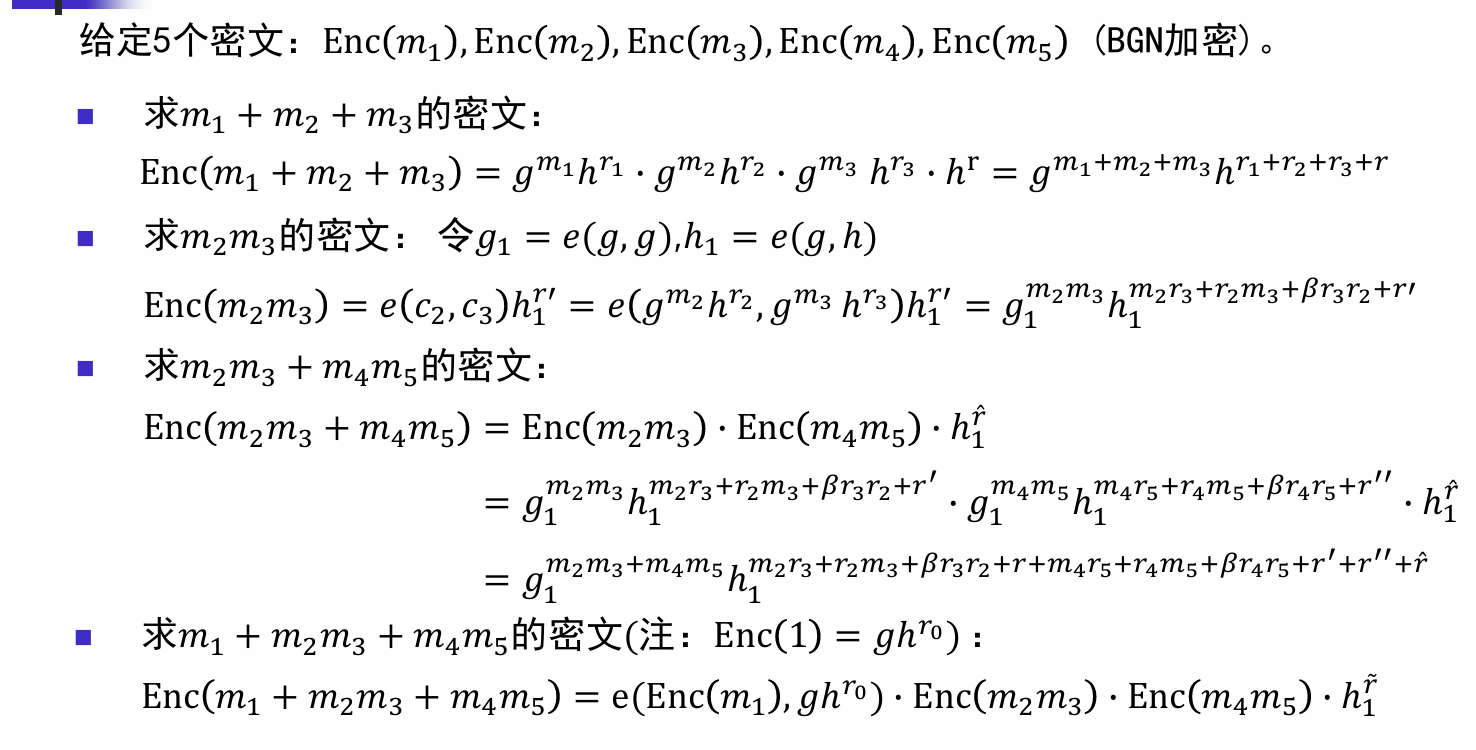Appearance
同态加密
Paillier加密: 任意次同态加与标量乘
支持无限次的加法同态以及明文k与密文的乘法同态(
参数设置:
- 选择两个大素数
,计算 - 计算
, , ,其中 为 的不同质因数 - 由二项式定理易知:
, ,易知: - 对于一个映射
是单射
证明
设
,则 ,则 ,设 ,则 ,如果 ,则 ,而 ,则 恒成立,但是对于模 而言,如果 ,则 ,故不成立,所以 ,即 ,从而 。证毕。 是一个同态 - 公钥为
, 私钥为 ,既 - 记
- 选择两个大素数
加密
- 选择随机数
- 明文
- 密文计算:
- 选择随机数
解密
- 计算
,则 , - 计算
(参数设置中的3) - 解得
- 计算
原始版本:把
同态加
- 设有两个密文
, - 则
- 设有两个密文
标量乘
- 设有密文
,标量 - 则
- 设有密文
BGN加密: 任意次同态加与一次同态乘
配对的一些性质:
乘法同态:
指数可提到映射外:
合起来:
密钥生成
- 选择两个大素数
,计算 - 准备双线性映射
,生成元 ,生成元 , - 公钥为
,私钥为
- 选择两个大素数
加密 计算
,其中 为明文, 为随机数 解密
- 计算
- 然后对其进行离散对数求解,得到
- 计算
同态加
同态乘
, denote
, ,有 ,