课程项目一：乘法程序

项目需求

程序简介

程序编译及运行环境

编译命令：

cwd:${fileDir}  
cd build  
cmake ..  
make

生成文件在项目根目录下,命名为Complex
系统环境：Ubuntu 24.04 LTS
g++ (GCC) 10.2.1 20200825 (Alibaba 10.2.1-3.8 2.32)

程序特点

支持任意位数的大数计算；支持对小数、科学计数法的输入与计算；支持对输出形式的格式化；完善的错误处理与提示机制；支持对微秒级的运行时间计时

程序功能

直接运行，显示操作提示
乘法运算
- 整数与整数
- 整数与小数
- 小数与小数
- 小数与科学计数法
- 科学计数法与科学计数法
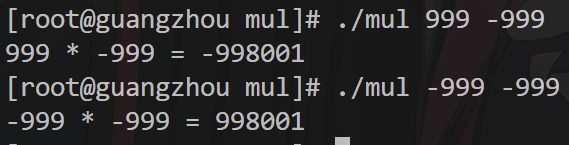
- 正负数运算
- 大数运算
支持参数
- -d 显示运算时间（非程序总运行时间）
- -e 使用科学计数法输出
- -p<num> 指定精确度
- -k 使用 Karatsuba 算法（图略）
- 不同参数可以组合使用，例如./mul num1 num2 -e -p2可以将常数部分截断到小数点后两位，参见大数计算的演示。
错误处理机制

程序实现与设计思路

数据输入处理

首先将全部输入转化为字符串，并使用正则表达式匹配输入是否合规

cpp

//检查输入是否为整型、浮点型或科学计数法
auto is_valid_number = [](const std::string& s) {
    std::regex number_pattern(R"(^[-+]?\d*\.?\d+([eE][-+]?\d+)?$)");
    return std::regex_match(s, number_pattern);
};
if (!is_valid_number(n1) || !is_valid_number(n2)){
    throw "Error: input is not a number";
}

由于要实现多种输入的计算，思路是把所有数据全部转换统一为纯数字的字符串，这样就能使用同样的算法来计算，并且还要储存小数点的位置以在输出时恢复数据的信息

cpp

/// @brief 处理小数点与科学计数法，将传入的字符串转换为纯数字字符串
/// @param s 需要处理的字符串
/// @return 十的次方
int Mul::precision_num(std::string &s) {
    int pre = 0;
    size_t e_pos = s.find_first_of("eE");
    if (e_pos != std::string::npos) {
        pre = std::stoi(s.substr(e_pos + 1));
        s = s.substr(0, e_pos);
    }
    size_t dot_pos = s.find('.');
    if (dot_pos != std::string::npos) {
        int a = s.length() - 1 - dot_pos;
        s = s.erase(dot_pos, 1);
        if(s[0] == '0'){
            s = s.substr(1);;
        }
        return -a + pre;
    }
    return pre;
}

例如1.0e10被转换为10，返回的pre为9；0.01被转换为01，返回的pre为-2

乘法运算

本程序选择使用高精度乘法和Karatsuba算法进行计算
高精度乘法既模仿竖式乘法的原理，将两个数的每一位分被相乘再相加，核心循环如下

cpp

    //从尾到头遍历第一个数的每一位
    for (int i = len1 - 1; i >= 0; i--) {
        int carry = 0;//进位
        int n1_digit = n1[i] - '0';

        i_n2 = 0;

        //从尾到头遍历第二个数的每一位
        for (int j
 = len2 - 1; j >= 0; j--) {
            int n2_digit = n2[j] - '0';
            /*模仿竖式相乘，n1_digit乘以n2_digit的每一位，carry存储进位数据，在下一轮循环中加入*/
            int sum = n1_digit * n2_digit + result[i_n1 + i_n2] + carry;
            carry = sum / 10;
            result[i_n1 + i_n2] = sum % 10;
            i_n2++;
        }

        if (carry > 0) {
            result[i_n1 + i_n2] += carry;
        }
        i_n1++;
    }

Karatsuba 则是在高精度乘法计算的基础上采用递归与分治的思想，将相乘的两数 n1、n2 不断划分为 a、b、c、d 四部分，以减少遍历的次数，把时间复杂度从 $O(n^2)$ 降为 $O(n {\log_2 3})$ 。

性能分析

在计算两个长度为512bits的整数时，使用常规高精度乘法的时间一般为0.0001微秒左右，使用-k参数调用Karatsuba算法的时间则在0.006-0.008微妙之间，推测是对字符串进行的操作太多的缘故。

在Python中，进行同样的运算只需2.0e-05 微秒左右，既0.001微秒可以复运算60次，查阅资料得知python在karatsuba算法的基础上还使用了ftttoom-cook算法进行加速。

遇到的困难

主要在数据处理与优化运算两方面

在数据处理方面上，由于在前期没有构思好思路，后期不愿重构前面的代码逻辑，导致在格式化输出数据时的代码编写十分困难。处理方案则为不断添加各种逻辑判断，这也使得该部分代码非常臃肿复杂。

在优化运算方面上，添加了Karatsuba算法，但效率反而不及直接计算，尝试使用内联函数来减少递归的调用，但效果不明显。最后发现编译器开启O3优化可以将代码运行时间缩短为三分之一，把512bits整数乘法的时间从0.003微秒减少到了0.001微秒

项目总结

程序目前有较为完善的功能，但后续有较大优化空间，例如可以将对字符串操作转换为对数组操作，将逻辑判断从if-else转换为switch语句等以提升运行效率。

课程项目一：乘法程序 ​

项目需求 ​

程序简介 ​

程序编译及运行环境 ​

程序特点 ​

程序功能 ​

程序实现与设计思路 ​

数据输入处理 ​

乘法运算 ​

性能分析 ​

遇到的困难 ​

项目总结 ​