基于Elgamal的端到端加密通信系统

✍️✍️✍️代码一定要备份✍️✍️✍️

✍️✍️✍️commit后一定要push✍️✍️✍️

😭😭😭

写于2025-5-25 因为一段傻逼cmake把代码删得啥都不剩 已红温

罪魁祸首

# make clean-all
add_custom_target(clean-all
    COMMAND ${CMAKE_COMMAND} -E remove_directory ${PROJECT_SOURCE_DIR}/test
    COMMAND ${CMAKE_COMMAND} -E remove_directory ${CMAKE_BINARY_DIR}
    COMMENT "清理所有构建文件和test文件夹"
)

项目简介

• 一个提供了html前端页面的端到端低创加密通信系统
• 项目地址

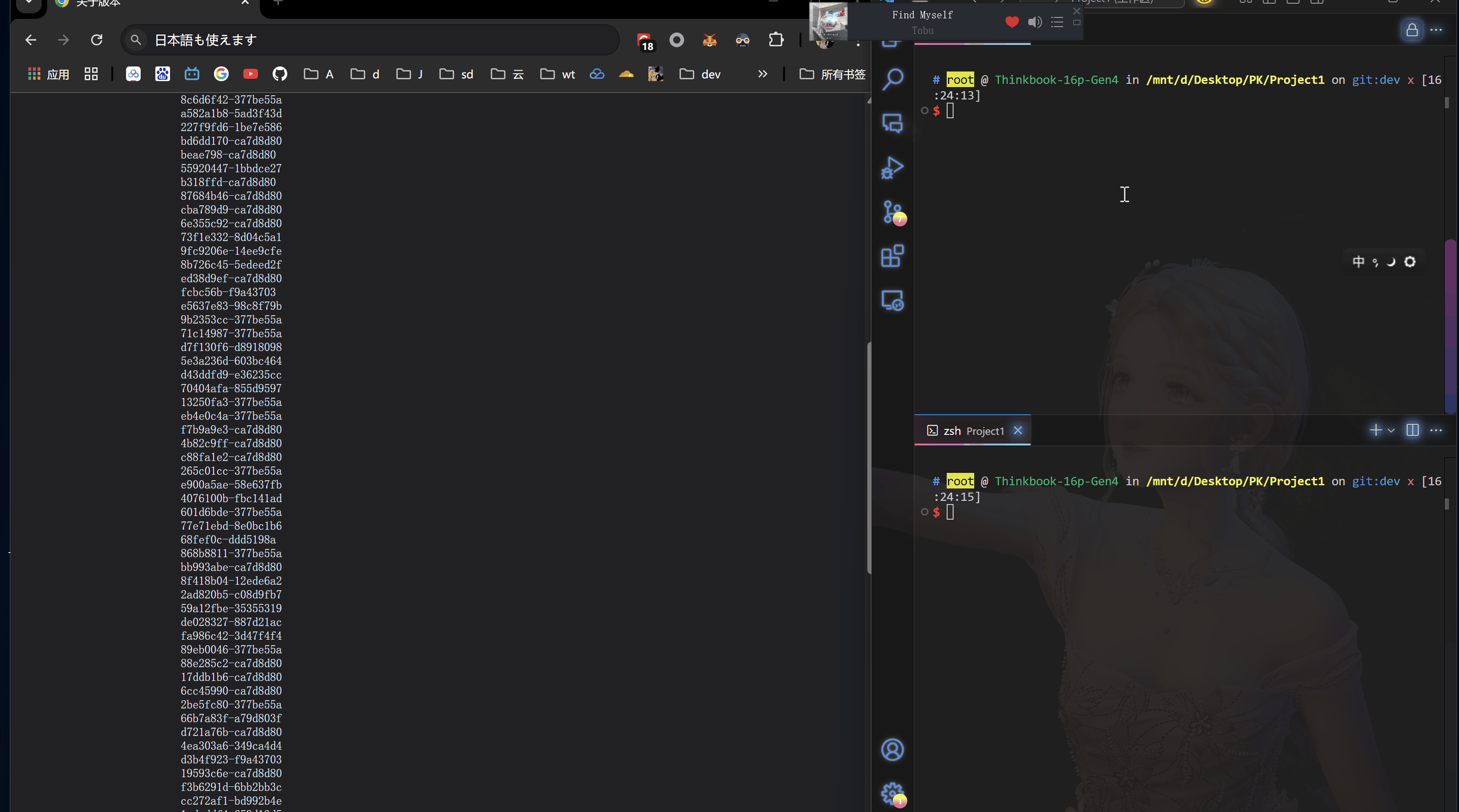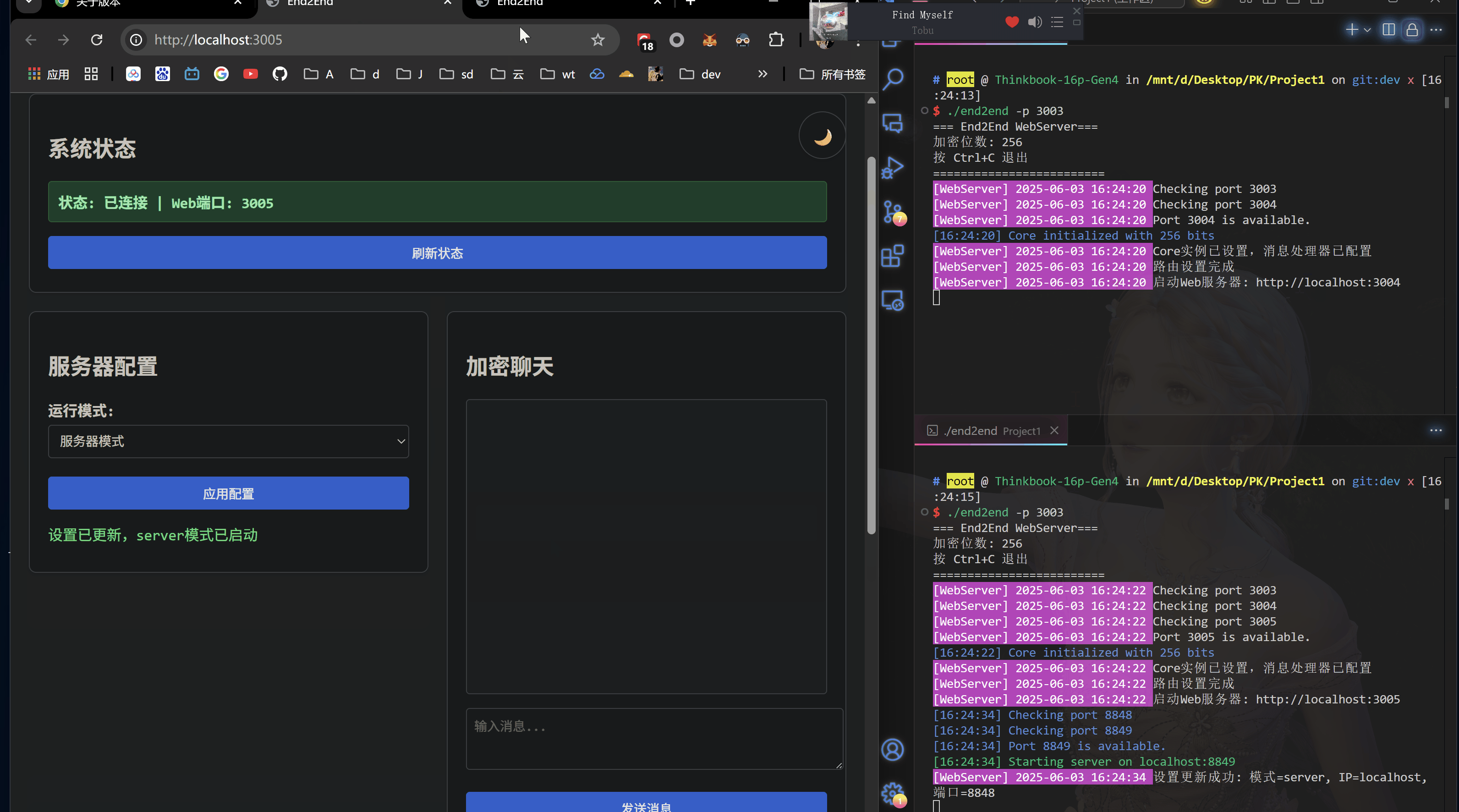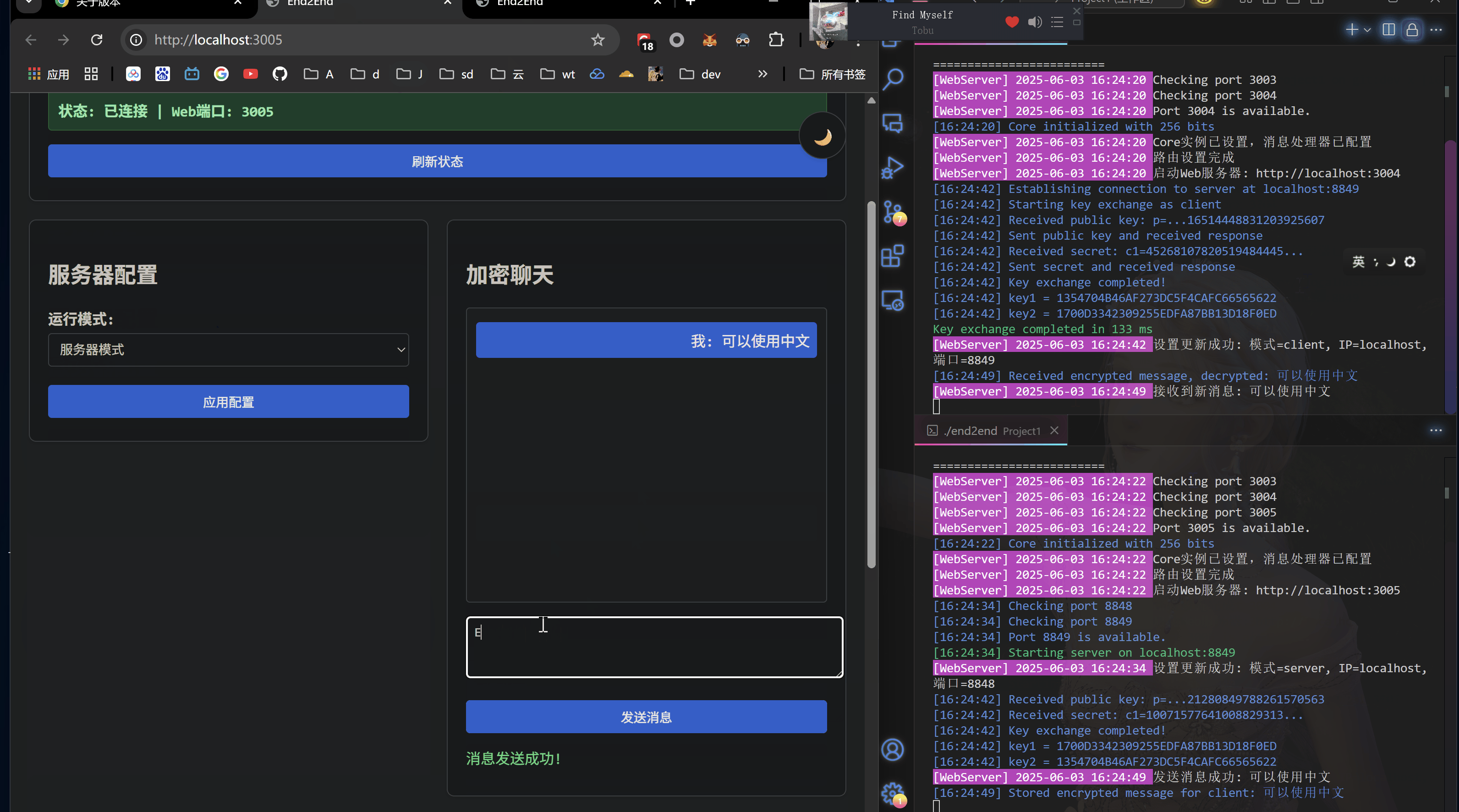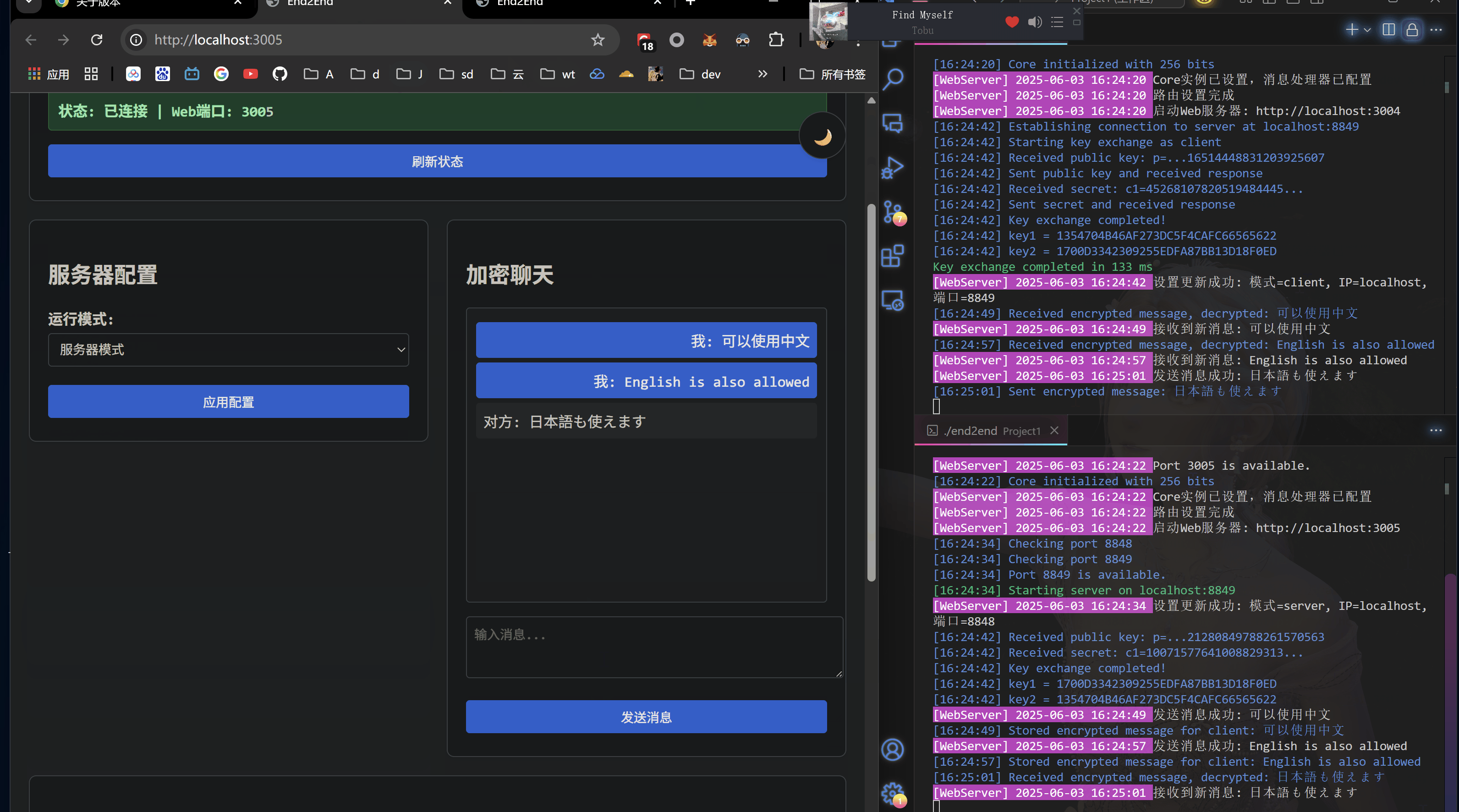
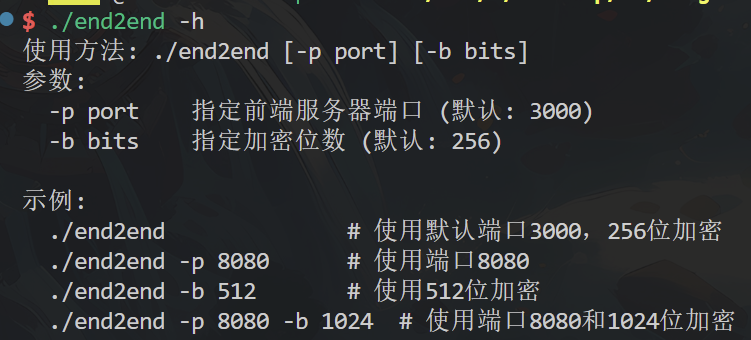
运行演示(./end2end)

项目特色

• 实现了基于http协议的Elgamal+SM4加密端到端通信
• 支持所有语言（只要std::string支持的都行理论上也支持传输文件）
• 满足OneWay——CPA以及IND-CPA安全性

项目编译

PS: 交叉编译配置太麻烦了，所以没整Windows端的

使用gmp作为大数运算库,在Ubuntu环境下进行编译，需要运行apt install libgmp-dev安装

• 编译环境:
• System Architecture: x86_64
• Linux Destribution: Ubuntu 24.04.1 LTS
• Linux Kernel: Linux 5.15.153.1-microsoft-standard-WSL2
• Cmake version: 3.28.3
• GNU Make version: 4.3

编译指令

# bin/zsh
cmake . && make
# 编译成功后可选: make clean-cache 清除中间文件

 -- Configuring done (0.2s)
 -- Generating done (0.8s)
 [ 35%] Built target core_lib
 [ 47%] Built target MillerRabin
 [ 58%] Built target elgamal
 [ 70%] Built target test_client
 [ 82%] Built target test_server
 [100%] Built target end2end

最后会在项目根目录下生成end2end，在/test目录下生成test_client、test_server、elgamal、MillerRabin共五个可执行文件。

素性检验

程序运行

• 可执行文件在test/MillerRabin
• 支持生成与判断任意位数的素数~~(理论上)~~
• 支持动态调整Miller-Rabbin的迭代次数
• 支持输出执行时间

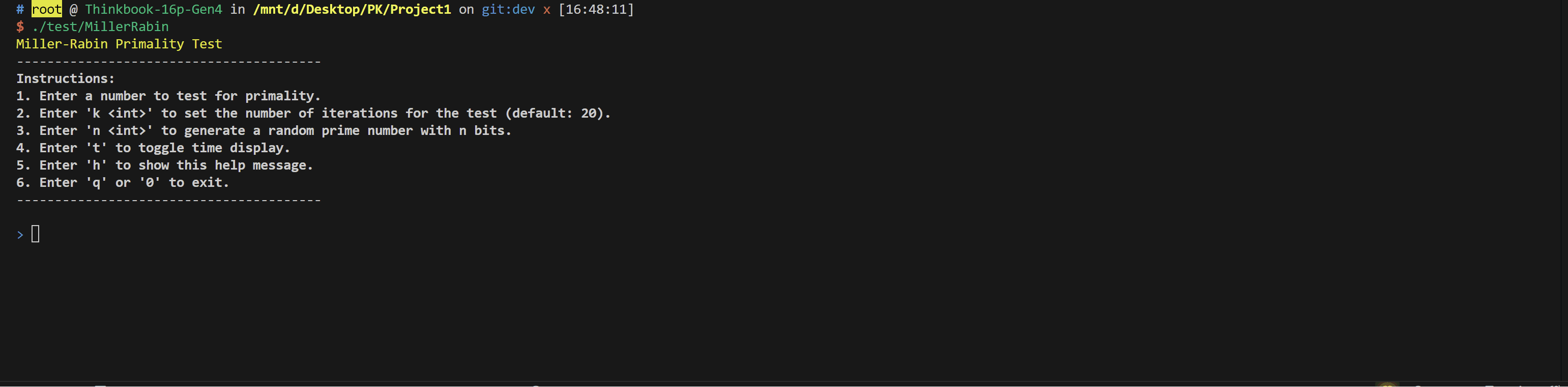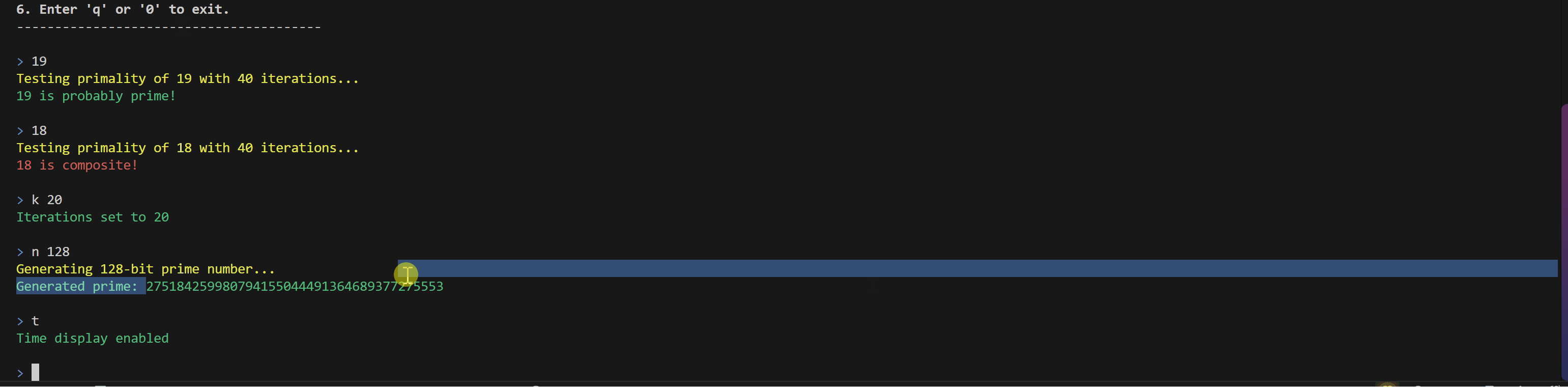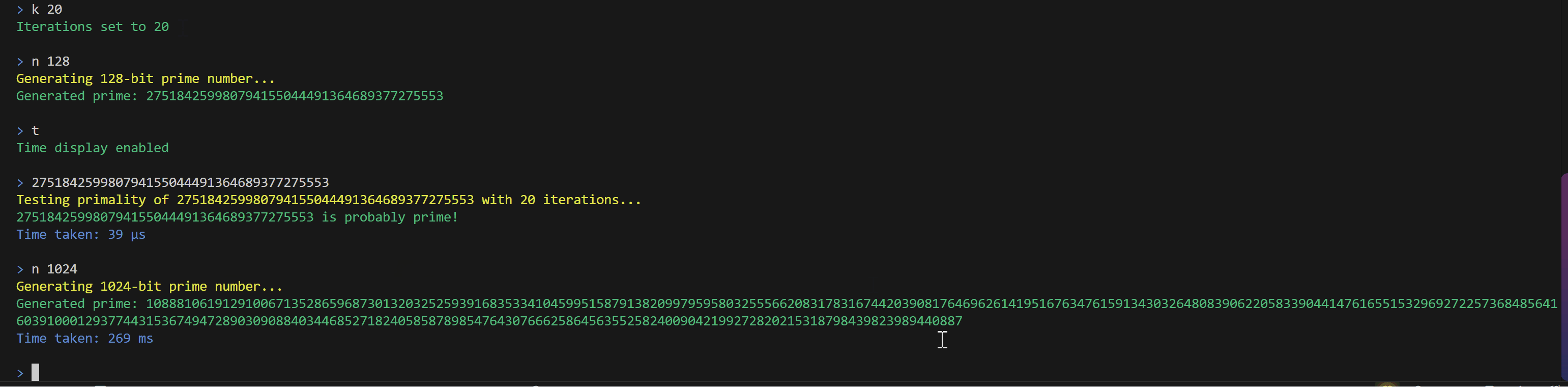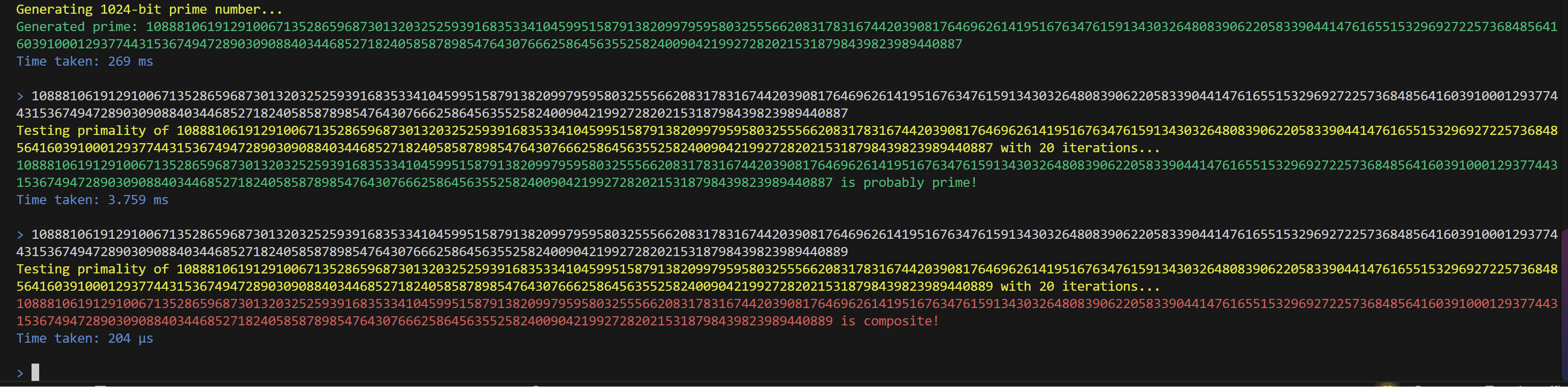
运行演示

程序实现与设计思路

• 使用gmp作为运算库
• 使用Miller-Rabin算法实现素数检验

Miller-Rabin实现 (getPrime/getPrime.cpp 63 - 141)

/// n: 需要检测的数
/// k: 检测轮数
bool MillerRabin(mpz_t n, int k)
{
    // 1. 将 n-1 写成 2^r * d 的形式
    mpz_t n_minus_1, d, temp, a, x;
    
    mpz_sub_ui(n_minus_1, n, 1); // n_minus_1 = n - 1
    mpz_set(d, n_minus_1); // d = n - 1
    
    int r = 0;
    while (mpz_even_p(d)) { // n-1 = 2^r * d
        mpz_fdiv_q_ui(d, d, 2); 
        r++;
    }
    
    // 使用全局随机数状态
    gmp_randstate_t& state = get_global_rand_state();
    
    // 2. 进行 k 轮测试
    for (int i = 0; i < k; i++) {
        // 生成随机数 a，范围 [2, n-2]
        mpz_sub_ui(temp, n, 3);  // temp = n-3
        mpz_urandomm(a, state, temp);  // ∈ [0, n-4]
        mpz_add_ui(a, a, 2);  // ∈ [2, n-2]
        
        // 计算 x = a^d mod n
        mpz_powm(x, a, d, n);
        
        // 如果 x = 1 或 x = n-1，则继续下一轮
        if (mpz_cmp_ui(x, 1) == 0 || mpz_cmp(x, n_minus_1) == 0) {
            continue;
        }
        
        // 进行 r-1 次平方
        bool composite = true;
        for (int j = 0; j < r - 1; j++) {
            mpz_powm_ui(x, x, 2, n);
            if (mpz_cmp(x, n_minus_1) == 0) {
                composite = false;
                break;
            }
        }
        
        if (composite) {
            // 清理内存
            mpz_clear(n_minus_1);
            mpz_clear(d);
            mpz_clear(temp);
            mpz_clear(a);
            mpz_clear(x);
            return false;
        }
    }

    return true;
}

性能分析

• 对于检查素数的MillerRabin函数，根据迭代轮数，在$k=20$时，检测一个$bits=2048$的数需要消耗约30ms，整体的时间复杂度为$O(k \cdot 2^n)$，其中n指被检测数的比特数。
• 而对于生成素数的getPrime函数(MillerRabin迭代轮数设置为40)，由于纯靠随机数去试，所以耗时较为不稳定，生成一个2048bits的素数时耗时一般在300ms~2000ms之间。

Elgamal加密算法

程序运行

• 可执行文件在test/elgamal
• 支持基于Elgamal与SM4-CBC模式的对于任意长度的文本加密

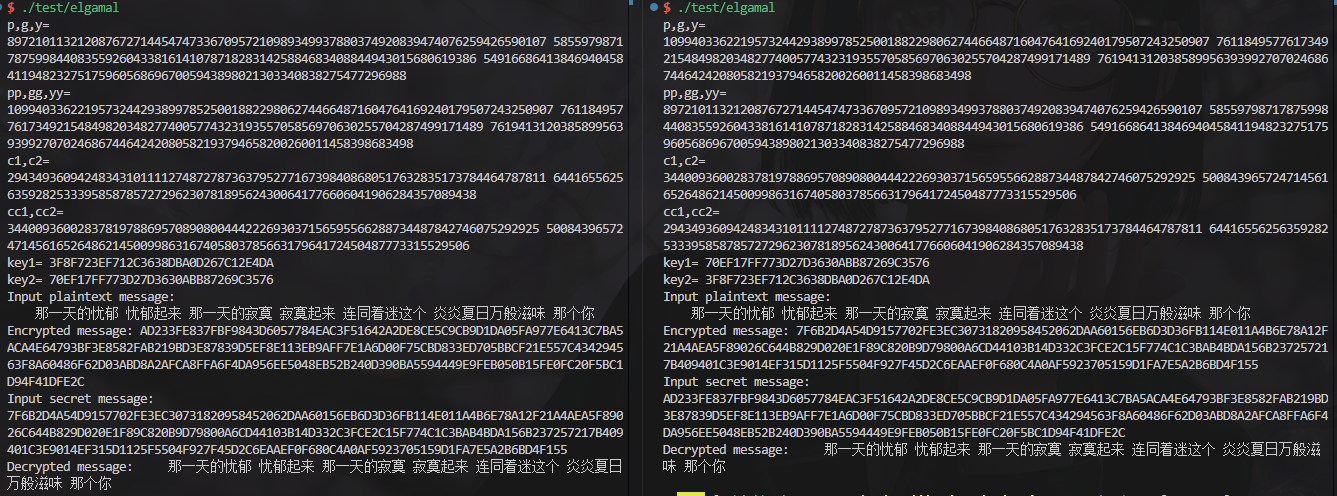
运行演示

程序实现与设计思路

1. Elgamal密钥生成

密钥生成算法如下

$\begin{aligned} & 1. \; \text{Gen a } (n-1) \text{ bits prime } q, \text{ let } p = 2q+1 .\\ & 2. \; \text{Choose a random int } h \in [2, p-1] .\\ & 3. \; \text{Calculate } g = h^{2} \; mod \; p , \text{ if } g>1, \text{ then accept as generator} .\\ & \quad \text{Proof: Since } p = 2q+1 \text{ and } q \text{ is prime, ord} (g) \text{ divides } \phi(p) = 2q .\\ & \quad \; \text{If } g^2 \neq 1 \; mod \; p, \text{ then } \text{ord}(g) \in \{q, 2q\} . \text{ Since } g = h^2, \text{ we have } \text{ord}(g) = q .\\ & 4. \; \text{Choose a random int } x \in [1, q-1] .\\ & 5. \; \text{Calculate } y = g^{x} \; mod \; p .\\ & 6. \; \text{The public key is } (p, g, y), \text{ private key is } x . \end{aligned}$

elgamal/elgamal.cpp 34 ~ 62

// gen p q g h x y
void ElGamal::keygen()
{
    // 1. 生成素数 p = 2q + 1
    genSafePrime(p, q, bits);
    
    // 2. 选取生成元 g
    mpz_t h, exp;
    mpz_inits(h, exp, NULL);
    mpz_set_ui(exp, 2); // exp = 2
    
    while (true) {
        // 生成随机数 h ∈ [2, p-1]
        mpz_urandomm(h, state, p);
        if (mpz_cmp_ui(h, 2) < 0) continue;
        
        // g = h^2 mod p
        mpz_powm(g, h, exp, p);
        if (mpz_cmp_ui(g, 1) > 0) break;
    }
    mpz_clears(h, exp, NULL);
    
    // 3. 生成私钥 x ∈ [1, q-1]
    do {
        mpz_urandomm(x, state, q);
    } while (mpz_cmp_ui(x, 1) < 0);
    
    // 4. 计算公钥 y = g^x mod p
    mpz_powm(y, g, x, p);
}

2. 随机数交换的实现

   1. 发送者调用Elgamal.getM(&m)函数生成明文在群中的随机数$\mathbb{m} \in [2,q-1]$
   2. 发送者调用Elgamal.encrypt(m,c1,c2)加密$\mathbb{m}$，发送[$c1 = g^k \;mod\; p$，$c2 = m \cdot y^k \;mod\; p$]
   3. 接收者调用Elgamal.decrypt(c1,c2,&m)，最终得到$m = c2 \cdot ({c1}^x \;mod\; p)^{-1} \;mod\; p$

elgamal/elgamal.cpp 94 ~ 138

void ElGamal::encrypt(mpz_t m, mpz_t c1, mpz_t c2)
{
    try {
        checkM(m);
    } catch (const std::invalid_argument& e) {
        throw;
    }
    
    mpz_t k;
    mpz_init(k);
    
    // 生成随机数 k ∈ [1, q-1]
    do {
        mpz_urandomm(k, state, q);
    } while (mpz_cmp_ui(k, 1) < 0);
    
    // 2. c1 = g^k mod p
    mpz_powm(c1, g, k, p);
    
    // 3. c2 = m * y^k mod p
    mpz_powm(c2, y, k, p);
    mpz_mul(c2, c2, m);
    mpz_mod(c2, c2, p);
    
    // 清理临时变量
    mpz_clear(k);
}

void ElGamal::decrypt(mpz_t c1, mpz_t c2, mpz_t m)
{
    // 创建临时变量存储中间结果
    mpz_t s;
    mpz_init(s);
    
    // 1. s = c1^x mod p
    mpz_powm(s, c1, x, p);
    
    // 2. m = c2 * s^(-1) mod p
    mpz_invert(s, s, p);
    mpz_mul(m, c2, s);
    mpz_mod(m, m, p);
    
    // 清理临时变量
    mpz_clear(s);
}

3. 消息加密的实现

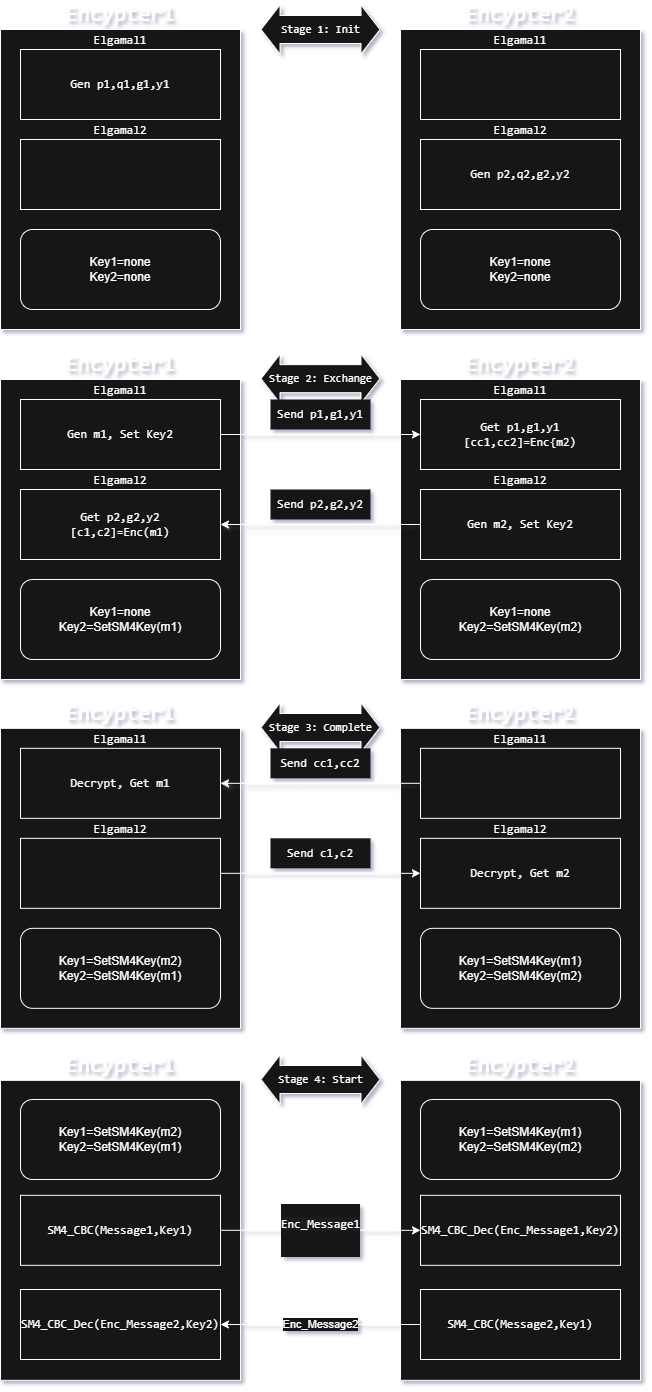
流程图

class MessageEncryptor{
public:
    MessageEncryptor(int bits);
    ~MessageEncryptor();

    void SendPKG(mpz_t p, mpz_t g, mpz_t y); 
    void GetPKG(mpz_t p, mpz_t g, mpz_t y);
    void ReceivePKG(mpz_t p, mpz_t g, mpz_t y); 
    void SendSecret(mpz_t c1, mpz_t c2); 
    void SetSM4Key(mpz_t m, int mode); // mode = 0, server; mode = 1, client
    void ReceiveSecret(mpz_t c1, mpz_t c2); 
    void EncryptMessage(const string& message, string& encrypted_message);
    void DecryptMessage(const string& encrypted_message, string& message);
    void GetSM4Key(string& key1, string& key2){
        key1 = sm4_key_server;
        key2 = sm4_key_client;
    }
    
private:
    int bits;
    ElGamal server; // server, 指'我'作为服务端接受请求
    ElGamal client; // client, 指'我'作为客户端发送请求
    string sm4_key_server;
    string sm4_IV_server;
    string sm4_key_client;
    string sm4_IV_client;
    string stringToHex(const string& input);   // 字符串转十六进制
    string hexToString(const string& hex);     // 十六进制转字符串
};

• 这部分的实现在encrypter下
• SM4算法代码来自于之前暑假写的一个小项目：基于MFC的实现SM3/4算法的GUI小程序

性能分析

测试代码在elgamal/test_elgamal.cpp

• 对于默认的$512bits$，生成公钥大概需要$100ms$~$761ms$，加解密则分别稳定在$60\mu s$和$35 \mu s$左右
• 而对于更大的$1024bits$，生成公钥的时间则更加不稳定，范围在$900ms$~$10000ms$乃至更多，加解密稳定在$400\mu s$和$200 \mu s$左右
• 由此可见程序时间消耗最主要在Elgamal.keygen()部分

网络通信的实现

程序运行

• 这里运行的文件为test_server和test_client

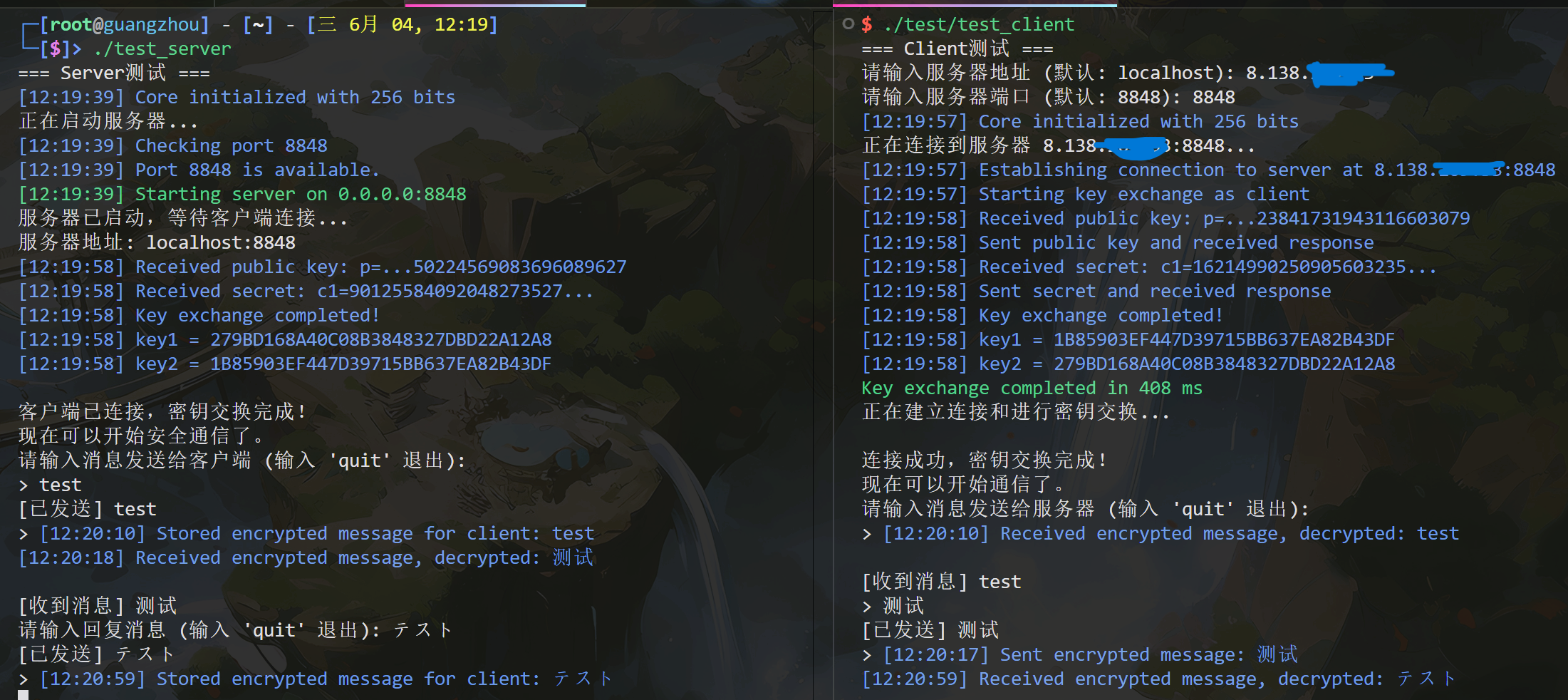
运行演示

程序实现与设计思路

• 这部分使用了httplib和nlohmann-json两个库
• 主要代码在core下
• Core对象分为Server和Client两种启动模式，对应的是常规的请求-响应模型
• 按道理说这种涉及双边通信的应该用Socket协议好点，但是因为后面要搞WebServer为了省事就都用http了
• 对于密钥交换的处理设置在/api/key_exchange端点下，流程跟上面Elgamal的是一样的，只不过把流程用http请求自动化了，代替了人手输入，实现如下：

core/core.cpp 153 ~ 203

void Core::handleKeyExchange(const httplib::Request& req, httplib::Response& res) {
    try {
        auto requestData = json::parse(req.body);
        string type = requestData["type"];
        
        if (type == "public_key") {
            if (receivePublicKey(requestData["data"])) {
                // 发送自己的公钥作为响应
                mpz_t p, g, y;
                mpz_inits(p, g, y, NULL);
                encryptor->SendPKG(p, g, y);
                
                json responseData;
                responseData["p"] = mpz_get_str(nullptr, 10, p);
                responseData["g"] = mpz_get_str(nullptr, 10, g);
                responseData["y"] = mpz_get_str(nullptr, 10, y);
                
                json response = createMessage("public_key", responseData);
                sendJsonResponse(res, response);
                
                mpz_clears(p, g, y, NULL);
            } else {
                sendJsonResponse(res, {{"error", "Failed to process public key"}}, 400);
            }
        } else if (type == "secret") {
            if (receiveSecret(requestData["data"])) {
                // 发送自己的密钥
                mpz_t c1, c2;
                mpz_inits(c1, c2, NULL);
                encryptor->SendSecret(c1, c2);
                
                json responseData;
                responseData["c1"] = mpz_get_str(nullptr, 10, c1);
                responseData["c2"] = mpz_get_str(nullptr, 10, c2);
                
                json response = createMessage("secret", responseData);
                sendJsonResponse(res, response);
                
                completeKeyExchange();
                mpz_clears(c1, c2, NULL);
            } else {
                sendJsonResponse(res, {{"error", "Failed to process secret"}}, 400);
            }
        } else {
            sendJsonResponse(res, {{"error", "Unknown key exchange type"}}, 400);
        }
    } catch (const exception& e) {
        log("Error in key exchange: " + string(e.what()));
        sendJsonResponse(res, {{"error", "Invalid request format"}}, 400);
    }
}

• 这里对于Client获取Server发送的信息采用轮询机制，Server维护一个消息列表，每次Client发送Get请求Server就更新列表并清除掉所有已经被请求的消息，坏处没有做身份认证导致谁都能发起这个Get请求，容易被干扰，但是好处是万一存在第三方监听就会被发现(

core/core.cpp

void Core::handleReceiveMessages(const httplib::Request& req, httplib::Response& res) {
    json messages = json::array();
    
    {
        lock_guard<mutex> lock(serverMessageMutex);
        while (!serverToClientMessages.empty()) {
            messages.push_back(serverToClientMessages.front());
            serverToClientMessages.pop();
        }
    }
    
    sendJsonResponse(res, {{"messages", messages}});
    updateLastActivity();
}

void Core::processMessageQueue() {
    while (running) {
        unique_lock<mutex> lock(messageMutex);
        messageCondition.wait(lock, [this] { return !outgoingMessageQueue.empty() || !running; });
        
        if (!running) break;
        
        while (!outgoingMessageQueue.empty()) {
            string message = outgoingMessageQueue.front();
            outgoingMessageQueue.pop();
            lock.unlock();
            
            // 加密消息
            string encryptedMessage;
            encryptor->EncryptMessage(message, encryptedMessage);
            
            if (mode == SERVER) {
                // 服务器模式：将消息存储到队列中等待客户端轮询
                lock_guard<mutex> serverLock(serverMessageMutex);
                serverToClientMessages.push(encryptedMessage);
                log("Stored encrypted message for client: " + message);
            } else {
                // 客户端模式：直接发送到服务器
                json requestData;
                requestData["encrypted_message"] = encryptedMessage;
                
                auto result = client->Post("/api/send_message", requestData.dump(), "application/json");
                if (result && result->status == 200) {
                    log("Sent encrypted message: " + message);
                } else {
                    log("Failed to send message: " + message, WARNING);
                }
            }
            
            lock.lock();
        }
    }
}

性能分析

• 性能瓶颈主要还是存在于Elgamal.keygen()上，故耗时和Elgamal中描述的差不多

程序优化

随机数生成优化

• 原先在每次调用getPrime和MillerRabin时都会重新初始化随机数生成器，后经过修改使用全局随机数状态（getPrime/getPrime.cpp 8 ~ 45），避免重复初始化开销。

快速幂算法选择

 

• 🕱🕱🕱这部分的被删完了，后面重写时就全都用gmp的mpz_powm了
• 原本使用的快速幂算法是自己编写的基本二进制幂算法（getPrime/getPrime.cpp 123 ~ 167），和gmp库提供的mpz_powm相比，在底数为$2^{41 \sim 43} \, bits$的情况下是自己编写的算法更优，但是偶然发现如果把miller_rabin函数的快速幂算法替换为mpz_powm（getPrime/getPrime.cpp 72 ~ 74）后，虽然getPrime的运算时间整体不变，但是如果后续继续调用快速幂算法时，运行时间会有较大提升，推测原因为CPU缓存预热以及mpz_powm是宏展开而非函数调用的原因。此处的代码在getPrime/test/test_mod.cpp

 Time taken (getPrime) : 170658061 nanoseconds
 Time taken (using mod_exp) : 1802 nanoseconds
 Result: 2667336
 Time taken (using mpz_powm) : 1965 nanoseconds
 Result: 2667336

使用自己实现的快速幂算法

 Time taken (getPrime) : 115933891 nanoseconds
 Time taken (using mod_exp) : 1901 nanoseconds
 Result: 3261320
 Time taken (using mpz_powm) : 587 nanoseconds
 Result: 3261320 

使用gmp库的快速幂算法

网络通信

• 原先在考虑密钥交换时设置了一堆端点，又复杂实现又慢，于是后面修改为了在同一端点下通过修改json头的形式来实现，使得路由设置更加简洁易懂

遇到的困难与解决思路

• 最大的困难其实还是写到一半时代码被删完了
• 主要在于设计密钥交换时的流程涉及的数据较多，需要一定时间去构思与理解
• 再这就是涉及网络通信时的线程管理不是很懂，最后还是靠ai解决了

总结

• 大体上还是实现了一个较为完整的项目，符合了最初的设想
• 对MillerRabin、Elgamal算法的实际应用与时间消耗有了更为直观的认识
• 大致掌握了gmp、httplib与C++_json的使用
• 后续有时间的话会考虑将密钥交换与信息传输的实现从http修改为socket