基于公钥密码的匹配系统

项目简介

一个使用同态加密方案的网恋匹配系统
项目地址

项目特性

对用户信息的完全保密：平台和使用者只能浏览到用户选择公开的内容，无法得用户选择加密的联系方式。
对用户选择的完全保密：配对双方只知道是否成功配对，无法知道配对失败的因是对方尚未做出回答/未浏览到此条推送，还是对方选择了拒绝配对；而台方也只能知道两个用户之间是否曾对对方做出过选择。
在配对成功后可自动获得对方的联系方式：使用对称加密的方式加密联系方式对加密密钥与配对选择进行同态绑定，只有双方都选择同意后才能获得对方的加密钥并且通过解密得到联系方式。
支持设置匹配偏好：使用关系数据库，通过构造Sql语句实现对匹配目标的件过滤与筛选，支持性别、年龄、学历等条件。

	A私钥	B私钥	A选择	B选择	A/B是否曾做出过选择	对方联系方式
A是否可知	✅	❌	✅	❌	❌	✅(仅在配对成功后)
B是否可知	❌	✅	❌	✅	❌	✅(仅在配对成功后)
平台是否可知	❌	❌	❌	❌	✅	❌

项目运行/编译

pipenv(推荐)

pipenv install -r requirements.txt
pipenv run python main.py

pip

pip install -r requirements.txt
pyhton main.py

项目结构

├── app # flask相关
│   ├── app.py # flask入口文件
│   ├── static
│   │   ├── css
│   │   ├── favicon.ico
│   │   └── js———
│   │           ├── CryptoJS # Google CryptoJS库
│   │           ├── fhe.js # 联系方式加密、选择加密的实现
│   │           └── secureElgamal.js # 登录、ELGamal公私钥生成实现
│   └── templates
│       ├── auth.html # 登录界面
│       └── index.html # 系统主界面
├── main.py # 主文件
├── main.spec # pyinstaller 配置文件
├── README.md
├── requirements.txt
├── utils
│   ├── api # api路由定义
│   │   ├── auth_routes.py
│   │   ├── __init__.py
│   │   ├── matching_routes.py
│   │   └── __pycache__
│   ├── auth # 登录认证相关
│   │   ├── auth_service.py
│   │   ├── __init__.py
│   │   ├── __pycache__
│   │   └── session_manager.py
│   ├── database # 数据库管理实现
│   │   ├── dataBase.py
│   ├── fhe # 平台fhe运算实现
│   │   ├── fhe_demo_v1.py
│   │   ├── fhe.py
│   ├── matching # 用户匹配推送
│   │   ├── __init__.py
│   │   ├── matching_service.py
│   │   ├── profile_service.py
│   ├── useful
│   │   ├── gen_rand_message.py
│   └── zk # 零知识登录
│       ├── dlogProof.py

程序实现与设计思路

技术路径

由于需要实现数据库操作并且后端操作比较复杂，还需要进行复杂数学运算，为了开发方便使用Python作为开发语言。~~毕竟现成的库多，打包也简单,,,~~
对于数据库方面，使用Python原生支持的SqpLite数据库，无需启动额外的数据库服务。

数据库结构：
account_data -- 存储用户名与用户公钥，初始化时会自带一个root用户存储全局的群参数
fhe_records -- 存储用户之间的加密选择和加密联系方式、加密后的加密密钥与同态运算结果
match_preference -- 存储用户匹配偏好 push_records -- 存储推送记录 session_ID -- 管理用户的session_ID user_data -- 存储用户的个人资料

对于后端部分，项目选择Flask作为http服务器与api服务器处理各种请求。
前端则使用纯html+js+css的方式实现。开始的时候被ai骗了，以为flask的模板渲染导致外部资源导入只能用flask的抽象方式，实际上用传统的导入方式就行，早知道用React或者Vue直接build出来一个静态网站就好了，后面也不用写的那么折磨
前端对称加密使用Google CryproJS库提供的AES-128实现。

注册阶段：用户通过种子生成512bits的ELGamal私钥，先通过api/register路由获取服务器启动时既生成的全局ELGamal群参数p,q,g，再通过api/complete_registration路由返回公钥y和用户名username完成注册。
登录阶段：用户从本地存储或服务器获取群参数，通过Fiat-Shamir启发式构造证明，服务器验证通过后返回24小时有效的SessionID。Reference

代码实现

python

 def dlogProof(x, g, p):
     # Step 1: Compute y = g^x (mod p)
     y = pow(g, x, p)

     # Step 2: Choose a random value r
     r = random.randint(1, p-1)

     # Step 3: Compute c = H(g, y, r) ← Fiat-Shamir启发式
     t = pow(g, r, p) # t = g^r (mod p)
     hash_input = str(g) + str(y) + str(t)
     c = int(SHA256.new(hash_input.encode()).hexdigest(), 16) % (p-1)

     # Step 4: Compute z = r + cx (mod p-1) 
     z = (r + c*x) % (p-1)

     # Step 5: Return the y and the proof pf = (c, z)
     return y, (c, z)

 def dlogProofVerify(y, g, p, pf):
     # Step 1: Unpack the proof
     c, z = pf

     # Step 2: Compute t = g^z / y^c  = g^r (mod p)
     y_c_inv = pow(pow(y, c, p), p-2, p)  # y^c的逆元
     t = (pow(g, z, p) * y_c_inv) % p

     # Step 3: Recompute challenge c' = H(g, y, t)
     hash_input = str(g) + str(y) + str(t)
     c_computed = int(SHA256.new(hash_input.encode()).hexdigest(), 16) %     (p-1)

     # Step 4: Return True if c == c_computed, else False
     return c == c_computed

通过SessionID，用户在进行各种操作时将SessionID附带在Authorization头中，而服务器通过require_session()函数验证身份，确保用户操作的合法性。

utils/api/auth_routes.py

python

 def require_session(self, f):
  """装饰器：要求有效的session"""
  @wraps(f)
  def decorated_function(*args, **kwargs):
      # 从请求头获取session ID
      session_id = request.headers.get('Authorization')
      if session_id and session_id.startswith('Bearer '):
          session_id = session_id[7:]  # 移除 'Bearer ' 前缀

      if not session_id:
          return jsonify({'error': 'Session ID required'}), 401

      db = self._get_db_manager()
      session_manager = SessionManager(db)
      username = session_manager.validate_session(session_id)

      if not username:
          return jsonify({'error': 'Invalid or expired session'}), 401

      # 将用户名添加到g对象中，方便路由函数使用
      g.current_user = username
      return f(*args, **kwargs)
 
  return decorated_function

用户资料更新

用户需要在完成个人资料后才能进行匹配，联系方式不会上传，仅仅以localStrorage的方式存储在本地方便用户填充。
用户可以选择是否设置匹配偏好，设置后系统只会推送满足条件的对象。

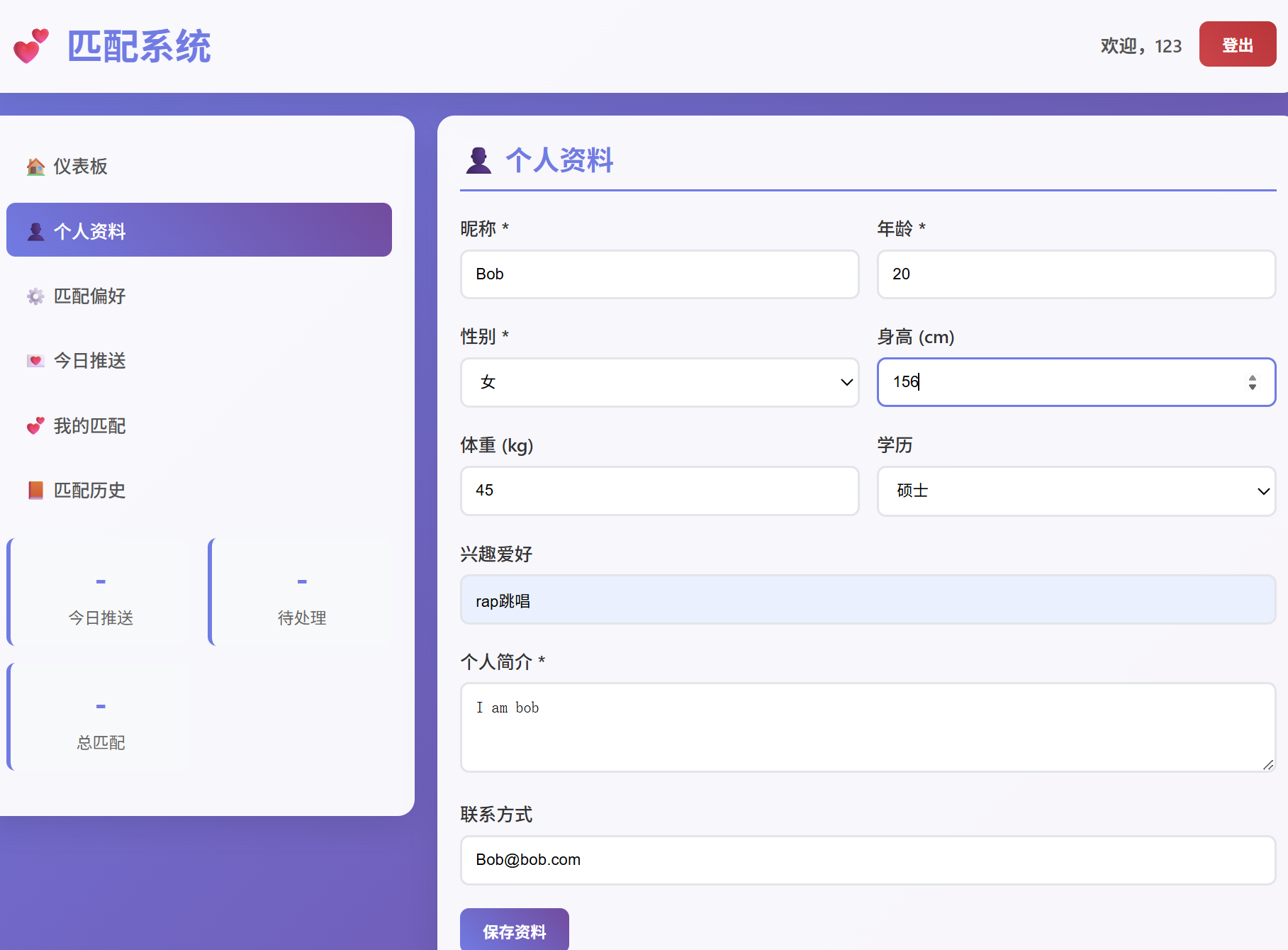
个人资料

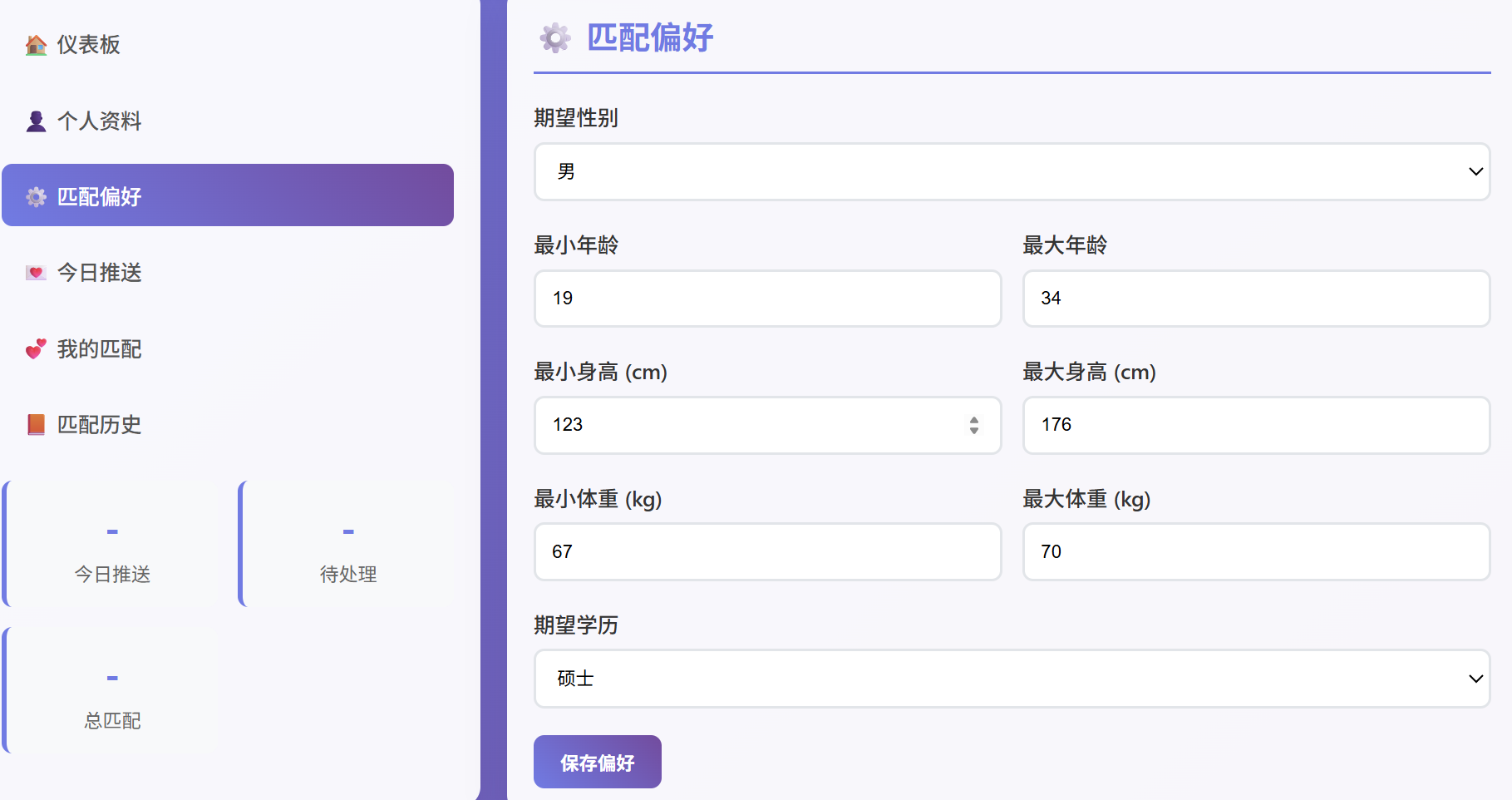
匹配偏好

匹配推送、选择加密与联系方式交换

流程

用户A获取到用户B的个人推送，包括B的个人信息，B的公钥y_b》（这里假设A先接到B的推送，而B还没接到A的推送）
用户A本地js计算，根据私钥计算共享的dh交换密钥 $y_{ab}$ 与共享的ELGamal私钥k，并且通过localStorage存储到本地。
用户A本地js计算，生成加密的联系方式，并且用交换密钥 $y_{ab}$ 加密联系方式。
用户A本地js计算，用户做出选择并且加密选择，如果接受加密明文1，拒绝则加密随机数。
用户A把加密后的联系方式和个人选择发送给服务器进行存储，服务器为二人之间创建一条fhe_record记录。
如果用户A这时候查询配对状态，服务器则会返回一串伪结果（包含伪造的选择同态乘法结果，伪造的同态绑定的加密方式密钥以及伪造的密文），用户A这时收到结果进行解密后也只会得到随机数（因为用户B还未做出选择）。
这时用户B收到用户A的推送，以同样的方式执行1~6，这时候服务器将两人状态标记为已经互相做出选择，进行同态运算。
在这时候，如果用户A或者用户B刷新状态，能够得到服务器返回的同态乘法结果以及同态绑定的联系方式加密密钥与联系方式加密密文。
这时候二人就可以在本地计算（decrypt_result）匹配结果，如果匹配成功，解密数字为1，则二者尝试解密对方的联系方式，完成配对与联系方式交换。

这样，服务器就无法知道二人的联系方式以及二人的选择情况，二人也无法知道自己没法解密的原因是因为对方没接到自己的推送还是对方拒绝了自己，从而保护用户隐私。

数学说明

每位用户选择一个私钥 $x$ ，计算 $y = g^x$ 后上传至平台。例如，Alice 选择 $x_A$ ，上传 $y_A = g^{x_A}$ ；Bob 选择 $x_B$ ，上传 $y_B = g^{x_B}$ 。如果平台推送两方进行匹配，那么Alice可以收到Bob的 $y_B$ ，Bob 也可以收到 Alice 的 $y_A$ ，Alice和Bob可以计算共享密钥 $k = g^{x_A \cdot x_B}$ ，后续双方的匹配选择，就可以借助 $k$ 进行加密。

利用 ElGamal 加密方案的同态性：

我们先回顾一下ElGamal加密方案（假设公共参数已经事先确定）：

公共参数： $(G, g, q)$ ，其中 $G$ 是循环群， $g$ 为生成元， $q$ 为群的阶。
密钥对： $(pk, sk)$ ，其中 $pk = h = g^x$ ， $sk = x$ 。
加密：输入明文 $M \in G$ ，随机选取 $k \in \mathbb{Z}_q$ ，输出密文 $(C_1, C_2) = (g^k, M \cdot h^k)$ 。
解密： $M = C_2 \cdot C_1^{-x}$ 。
同态性质：
- 相乘： $\text{Enc}(M_1) \cdot \text{Enc}(M_2) = \text{Enc}(M_1 \cdot M_2) = (g^{k_1 + k_2}, M_1 \cdot M_2 \cdot h^{k_1 + k_2})$
- 幂运算： $\text{Enc}(M)^r = \text{Enc}(M^r) = (g^{k \cdot r}, M^r \cdot h^{k \cdot r})$

双方可通过哈希函数等密钥派生函数 $H$ 从共享密钥 $k$ 派生出 $x = H(k) \in \mathbb{Z}_q$ ，作为用于ElGamal 加密的共享私钥（此私钥为两方共同持有）。

用户将自己的匹配选择加密后提交平台：

若选择接受，对明文 $M = 1$ 进行加密。
若选择拒绝，对随机选取的 $M \in G$ 进行加密。

平台在接收到双方密文后，进行密文同态乘法运算。若双方均选择接受，则密文为加密的 $1$ ，匹配成功；若任一方拒绝，则结果为群中随机元素，匹配失败。

也就是，平台在不知道双方选择的情况下，可以进行密文上的匹配运算。如果双方得到匹配后的运算结果，因为双方都持有私钥，那么双方都可以进行解密，得到最后的匹配结果（ $1$ 或者随机元素）。

值得注意的是，进行简单的密文上的乘法是不够的，假设 Alice 提交的密文是 $C_A$ ，在获得两个密文相乘的结果密文 $C_{\times} = C_A \cdot C_B$ 后，可以反推出Bob的密文 $C_B$ ，获得对方的加密选择，并解密。

为防止单方根据最终密文推断出对方的选择，平台需对同态计算后的密文进行再随机化：对密文做一次幂运算。例如，选择随机数 $r$ ，将密文对应的明文 $M$ 变换为 $M^r$ 。若 $M = 1$ ，则 $M^r = 1$ ，保持不变；若 $M$ 为随机值，则 $M^r$ 仍为随机元素，不可用于推断原值。

最终，匹配双方可解密密文获取匹配结果：

解密为 $1$ ：匹配成功。
解密为随机元素：匹配失败。

所以，以上思路可以同时解决上述两个问题。

联系方式交换：

用户除了上传加密匹配选择外，还上传一个用 ElGamal 加密的密码（如用于解密联系方式的对称密钥，或者某个带加密功能文件的口令），记为 $C_m$ ，以及一个用该密码加密的联系方式密文/文件。平台对匹配结果密文与 $C_m$ 进行同态乘法：

匹配成功（密文对应明文为 $1$ ）：结果仍为加密的原始密钥，双方可解密后获取联系方式；
匹配失败（密文为随机元素）：结果为无效密钥，无法解密获取联系方式。

运行界面展示

匹配推送

推送历史

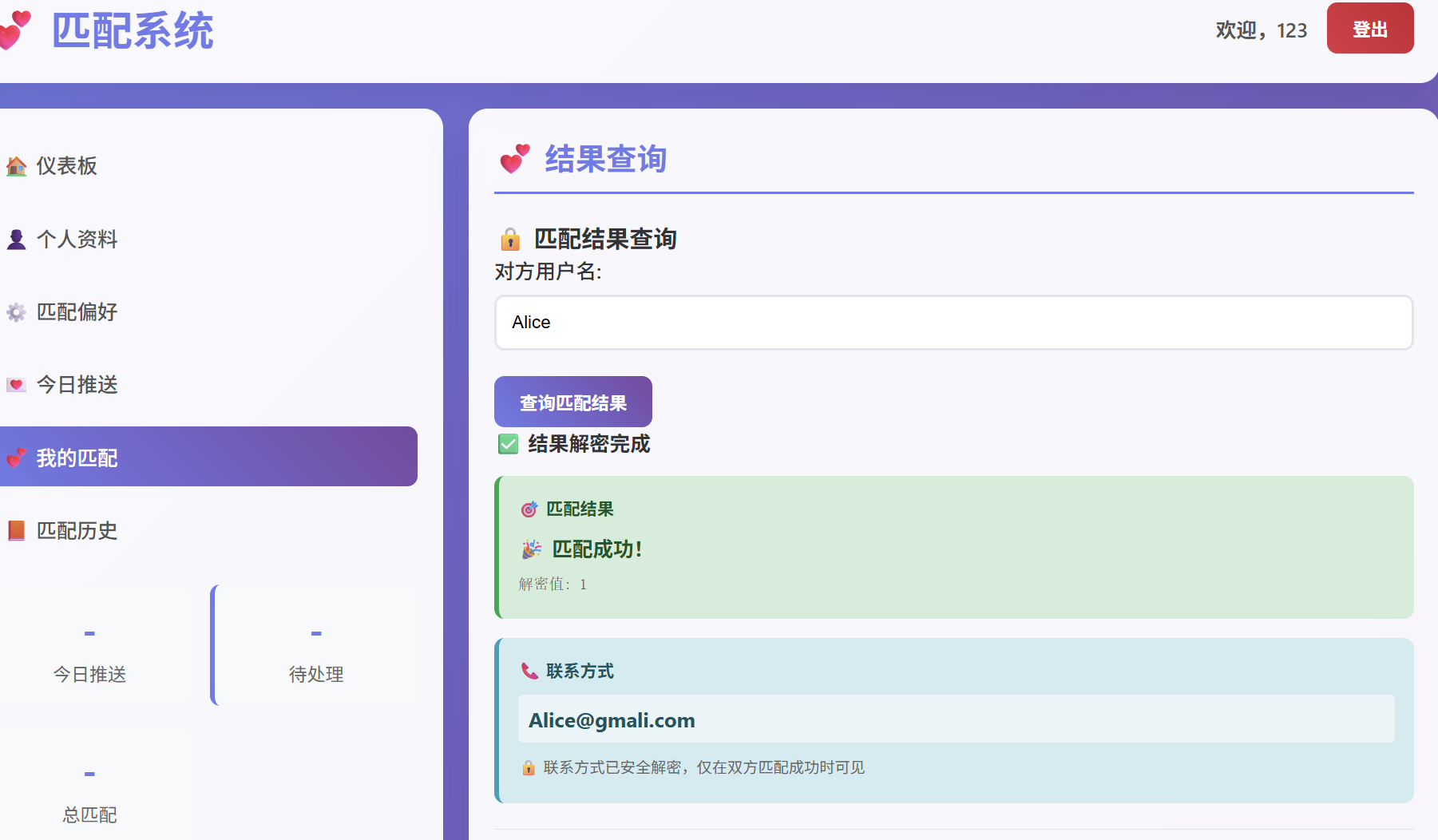
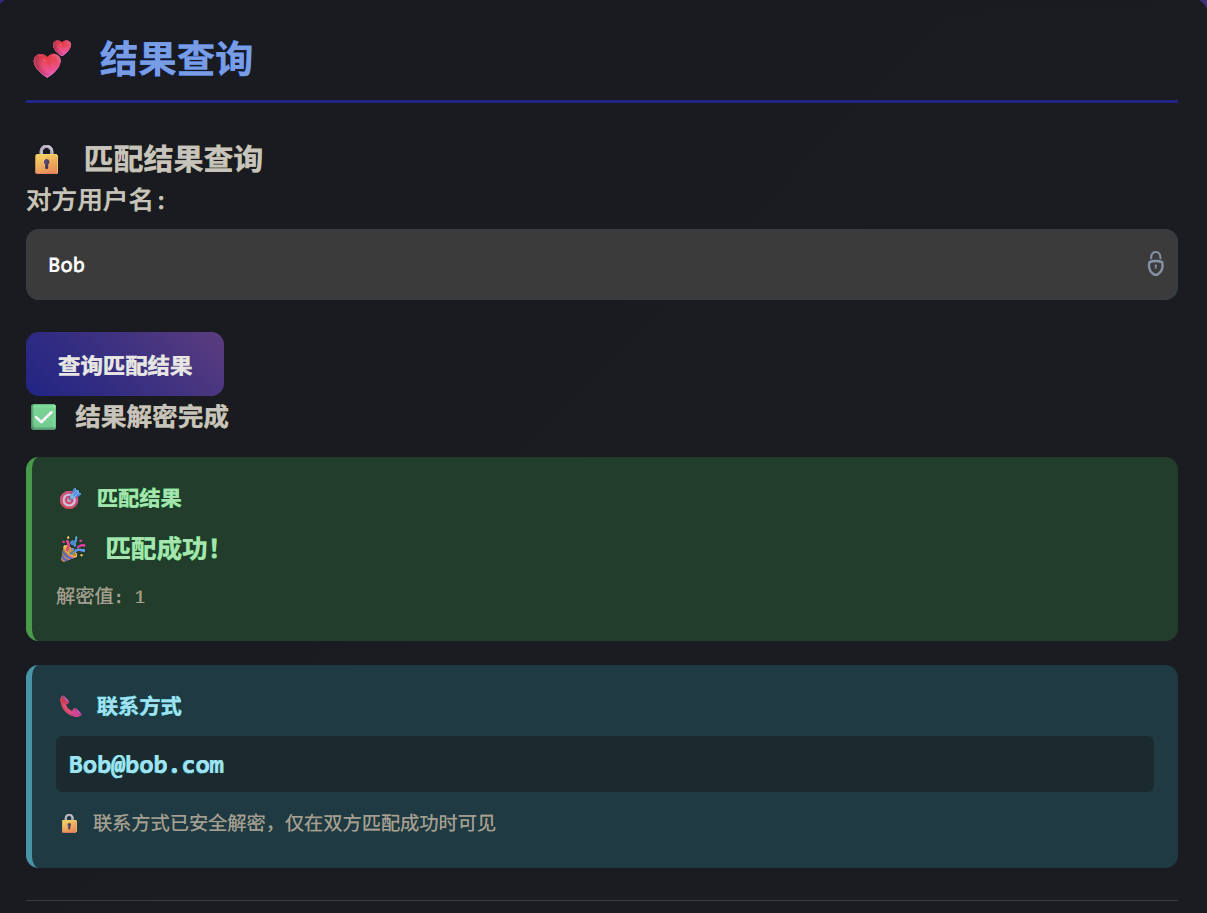
匹配成功

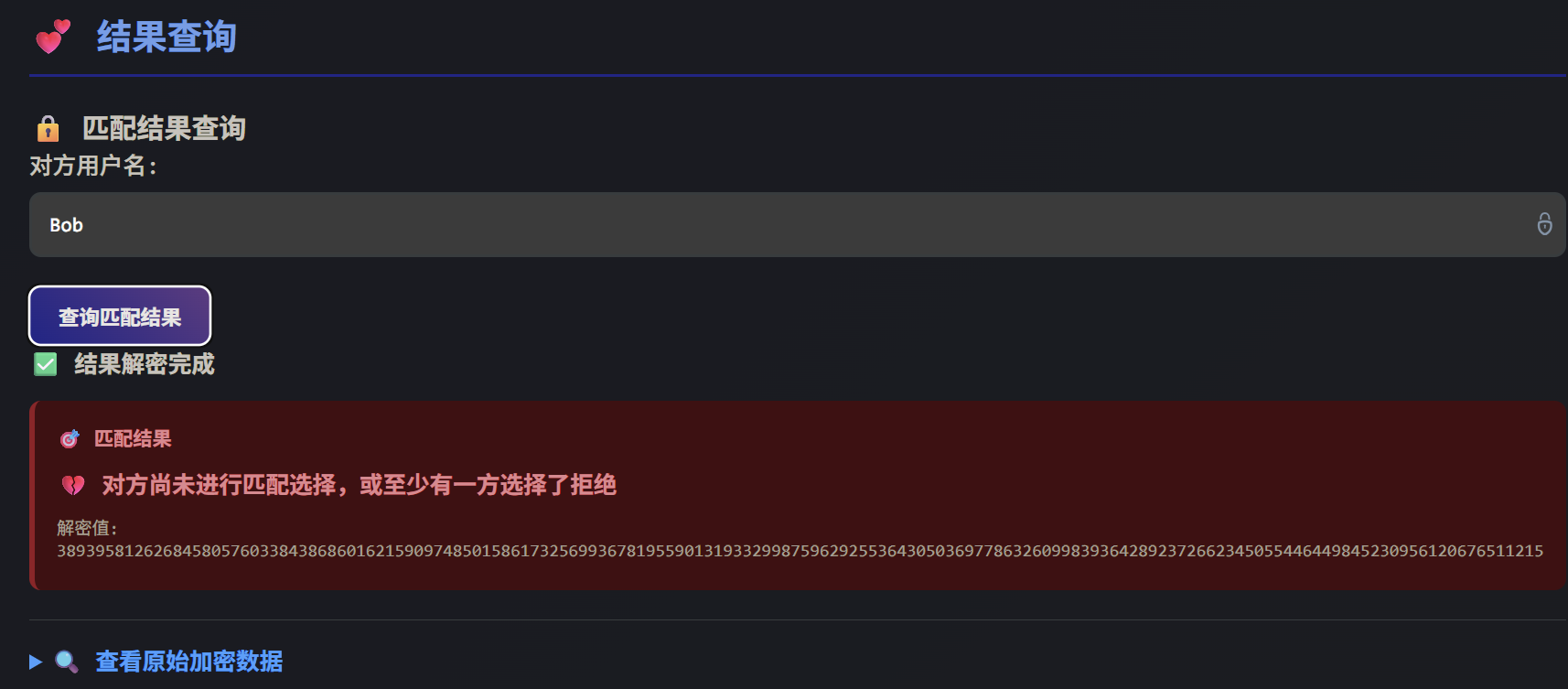
匹配失败

程序优化方向

当前系统最大的问题在于session_ID是明文传输，容易导致泄露从而被中间人攻击；而每次鉴权都使用数学运算的话显然又不现实，最简单的解决方案是加个SSL就能解决。
再有就是项目的层次逻辑过于混乱，需要进一步优化。在/api目录下原先的设想是仅仅做路由的定义，但是后面就一股脑把函数的实现也加进去了，导致每个文件都非常臃肿复杂，还有一堆不知道用不用得上的代码在项目里。
由于为了方便debug和省事，前端写了一堆localStorege又没写清理函数，登两三个账号后本地就容易留十几条记录，需要优化管理。

遇到的困难与解决思路

主要在于是第一次这么复杂的项目，前后端有十几个路由要实现，同时还要操作数据库，对于FHE的实现既要在后端Python中实现又要在前端的JS中实现，方案描述起来很容易，但是到了具体实现上经常容易整头晕，特别是由于同时设计双端导致每次这里改一点另外一个地方又报错了，只能慢慢加log来排，而且每次debug都要删掉数据库再重新初始化一遍才行，导致总是要花很多时间才找出来是哪里出了问题。

总结

~~不写cjs，不写ejs，不用vue，不用react，是真男人就要写纯js~~
~~深刻感受到ai毕竟还是替代不了人类的现实，毕竟ai是真理解不了和写出来这一坨💩山代码~~

写这种大项目之间一定要先规划好项目流程，定好需求，提前确定好路由沟通之间的json格式和数据库的结构，要不然后面再慢慢改是真的折磨。
中间有好几次想着直接开摆交个本地模拟的演示就算了，但是最后还是靠着五天时间慢慢磨完了，🤓不过写完之后是真的不想再见到这一坨抽象代码了。~~但不管怎么说也算是完成了一个拿得出手的项目(~~

基于公钥密码的匹配系统 ​

项目简介 ​

项目特性 ​

项目运行/编译 ​

项目结构 ​

程序实现与设计思路 ​

技术路径 ​

登录 ​

用户资料更新 ​

匹配推送、选择加密与联系方式交换 ​

流程 ​

相关代码 ​

运行界面展示 ​

程序优化方向 ​

遇到的困难与解决思路 ​

总结 ​