Basic

信息消息信号

信息的度量：信息量

信息量定义：对发生概率为$p(X)$的事件$X$，其信息量定义为：

$$I(X)=-{\log }_{2}p(X)$$

抛硬币：$p(X)=\frac{1}{2}$，信息量：$I(X)=-{\log }_2\frac{1}{2}=1\mathit{bit}$

简单说，对于bit由于只有01两种状态，故对于一个概率为1/2的事件，其信息量为1bit，而对于概率为1的事件，其信息量为0bit，$-{\log }_{2}0.001\approx 9.97bit$。

信息量与熵

熵：平均信息量

定义

设概率为$p(x)$,则熵定义为：

$$H(X)=-\sum _{x\in X}p(x){\log }_{2}p(x)$$

如果是确定性事件 $P(x)=1$ ，则$H(X)=-1\times {\log }_{2}1=0$，没有不确定性。

离散变量计算：

$$H(X)=-\sum _{i=1}^{n}p(x_i){\log }_{2}p(x_i)$$

e.g.：抛硬币：$H(X)=-\frac{1}{2}{\log }_2\frac{1}{2}-\frac{1}{2}{\log }_2\frac{1}{2}=1\mathbb{bit}$ 信息熵最大

e.g.2:

e.g.3:

设有千字文，每一字从万字表中选，求一篇的信息量：

总共有：${100000}^{1000}={10}^{4000}$ 篇文章

信息量为：$H(X)=-{10}^{4000}\times \frac{1}{{10}^{4000}}{\log }_2\frac{1}{{10}^{4000}}={\log }_2{10}^{4000}\approx 13288.97\mathit{bit}$

信源

对于一个二元信源:

$$\left(\begin{array}{c}X\\ P\end{array}\right)=\left(\begin{array}{cc}0& 1\\ p& q\end{array}\right)$$

如果横轴是概率 $P$，纵轴是熵 $H$，则曲线近似于一个对称轴为 $P=0.5$ 的抛物线，在 $P=0$ 和 $P=1$ 时，熵为0，在 $P=0.5$ 时，熵最大为1。

对于一个n元信源，熵取值范围为 $0\le H(X)\le {\log }_{2}n$，当且仅当各符号概率相等时，熵达到最大值 ${\log }_{2}n$。

而对于一个加密算法而言，熵越大，破解难度越大。假设有一个映射 $P\to C$，其中$P$为明文，$C$为密文，显然在为双射时，即每个明文对应唯一密文时，熵最大。

联合熵

表示 $X$ 和 $Y$ 同时发生时的不确定性：

$$H(X,Y)=-\sum _{x\in X}\sum _{y\in Y}p(x,y){\log }_{2}p(x,y)$$

e.g.:

$H(X,Y)=-4\times 0.25\times lo{g}_{2}0.25=2$

条件熵

表示在已知$Y$的条件下，$X$的不确定性：

$$H(X|Y)=-\sum _{x\in X}\sum _{y\in Y}p(x,y){\log }_{2}p(x|y)$$$$H(X|Y)=\sum _{j}p(x)H(X|Y=y_j)$$

可用以下公式计算：

$$\divideontimes H(X,Y)=H(Y)+H(X|Y)=H(X)+H(Y|X)$$

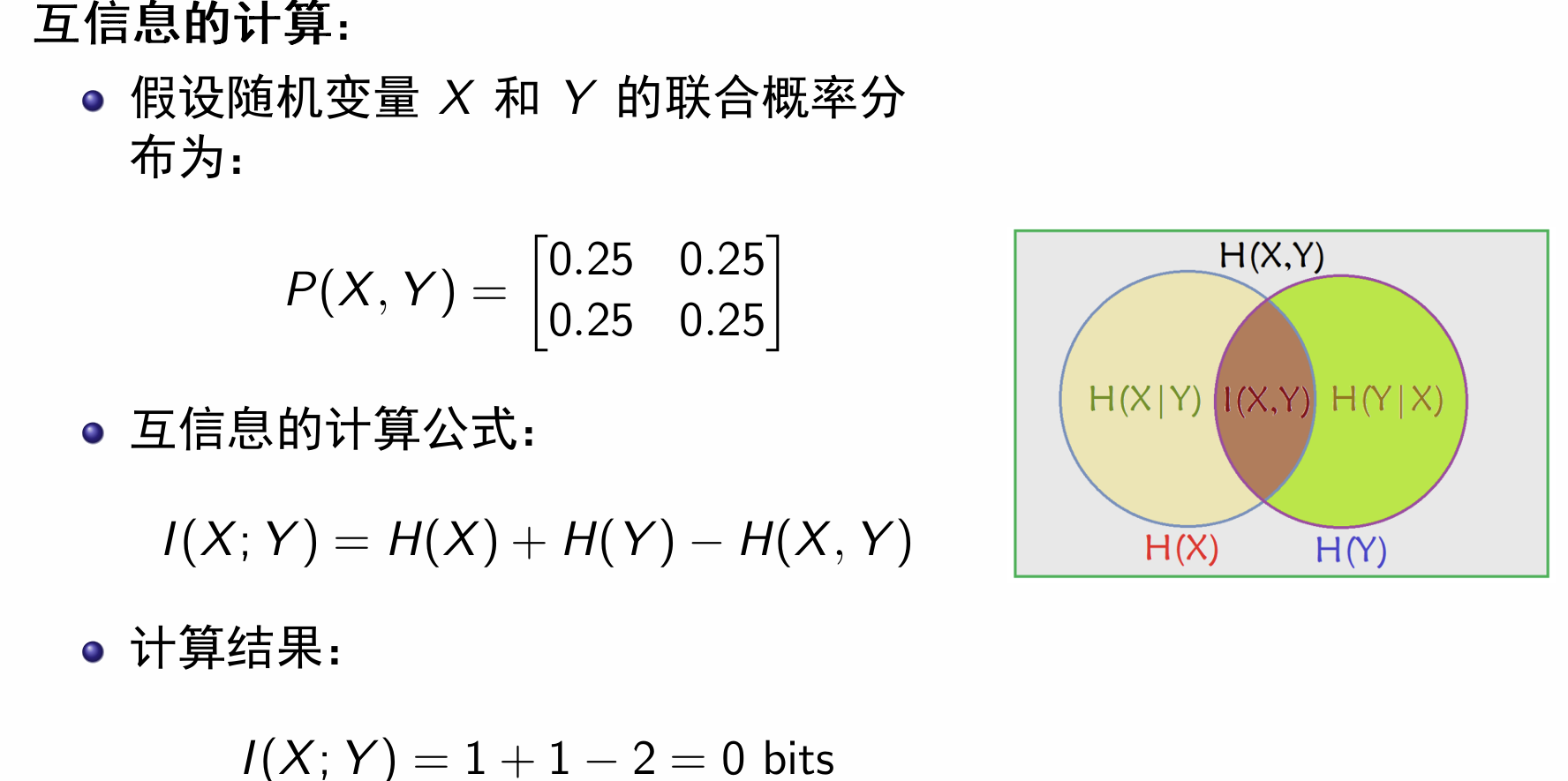
互信息

定义：

$$I(X;Y)=\sum _{x\in X}\sum _{y\in Y}p(x,y){\log }_2\frac{p(x,y)}{p(x)p(y)}$$

推导有：

$$I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)$$

信源编码

作用：信息压缩

香农第一定律

$$H(X)\le \overline{L}<H(X)+1$$

其中 $\overline{L}$ 为平均码长

信源编码定理

设信源$X$的熵为$H(X)$，则对于任意$\epsilon >0$，存在一个信源编码，其平均码长$\overline{L}$满足：