R1CS和QAP

R1CS定义

Rank-1 Constraint System 提供了一中将任意计算转化为一组多项式约束的方法。一个 R1CS 由一组约束组成，每个约束可以表示为一个向量方程：

$(a \cdot w) \times (b \cdot w) = (c \cdot w)$

其中：

• w 是一个包含所有变量（包括输入、输出和中间变量）的向量。
• a、b 和 c 是与 w 维度相同的系数向量。
• 这个等式被称为“Rank-1”是因为左边是两个线性项（a·w 和 b·w）的乘积，这形成了一个秩为 1 的二次型。

e.g.

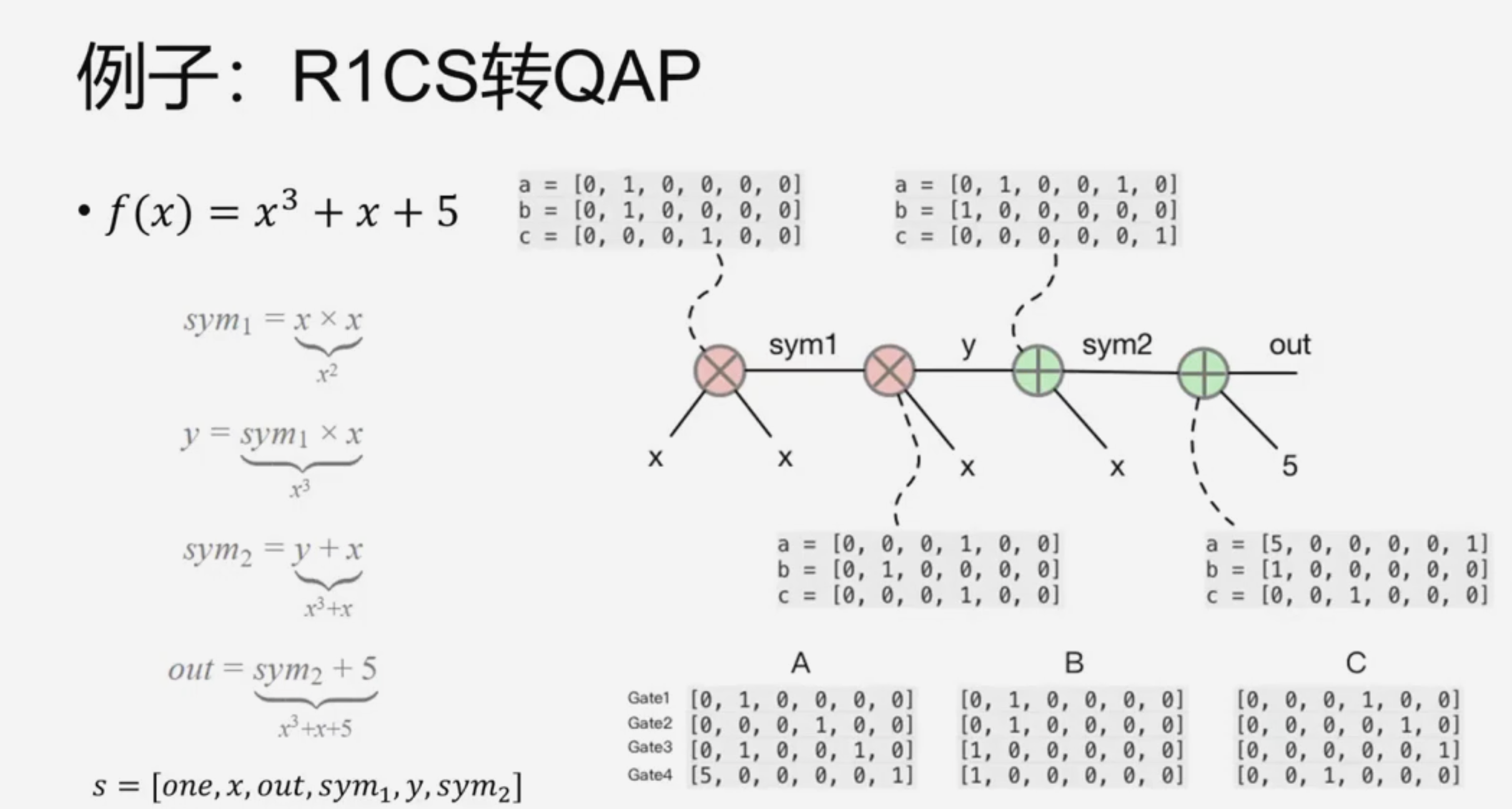
假设我们想证明我们知道一个值 x，使得 x³ + x + 5 = 35。

我们可以将这个计算分解成一系列简单的约束（通常是加法和乘法门）：

• x * x = x² （计算 x 的平方）
• x² * x = x³ （计算 x 的立方）
• x³ + x = x³ + x （加法）
• x³ + x + 5 = 35 （加常数并等于结果）

现在，我们为第一个约束 x * x = x² 构造一个 R1CS 约束。

定义变量向量 w = [1, x, x², x³, ...] （这里我们只关心前三个）。

约束：x * x = x²

我们需要找到向量 a, b, c 使得 (a·w) * (b·w) = c·w。

a·w 应该等于 x → a = [0, 1, 0, ...] (只有 x 的系数是 1)

b·w 应该等于 x → b = [0, 1, 0, ...] (同上)

c·w 应该等于 x² → c = [0, 0, 1, ...] (只有 x² 的系数是 1)

所以，这个约束的 R1CS 表示为（扁平化）：

a = [0, 1, 0, ...]

b = [0, 1, 0, ...]

c = [0, 0, 1, ...]

当 w = [1, x, x², ...] 代入时，(a·w)=x, (b·w)=x, (c·w)=x²，等式 x * x = x² 成立。

整个计算过程会被分解成多个这样的 R1CS 约束。

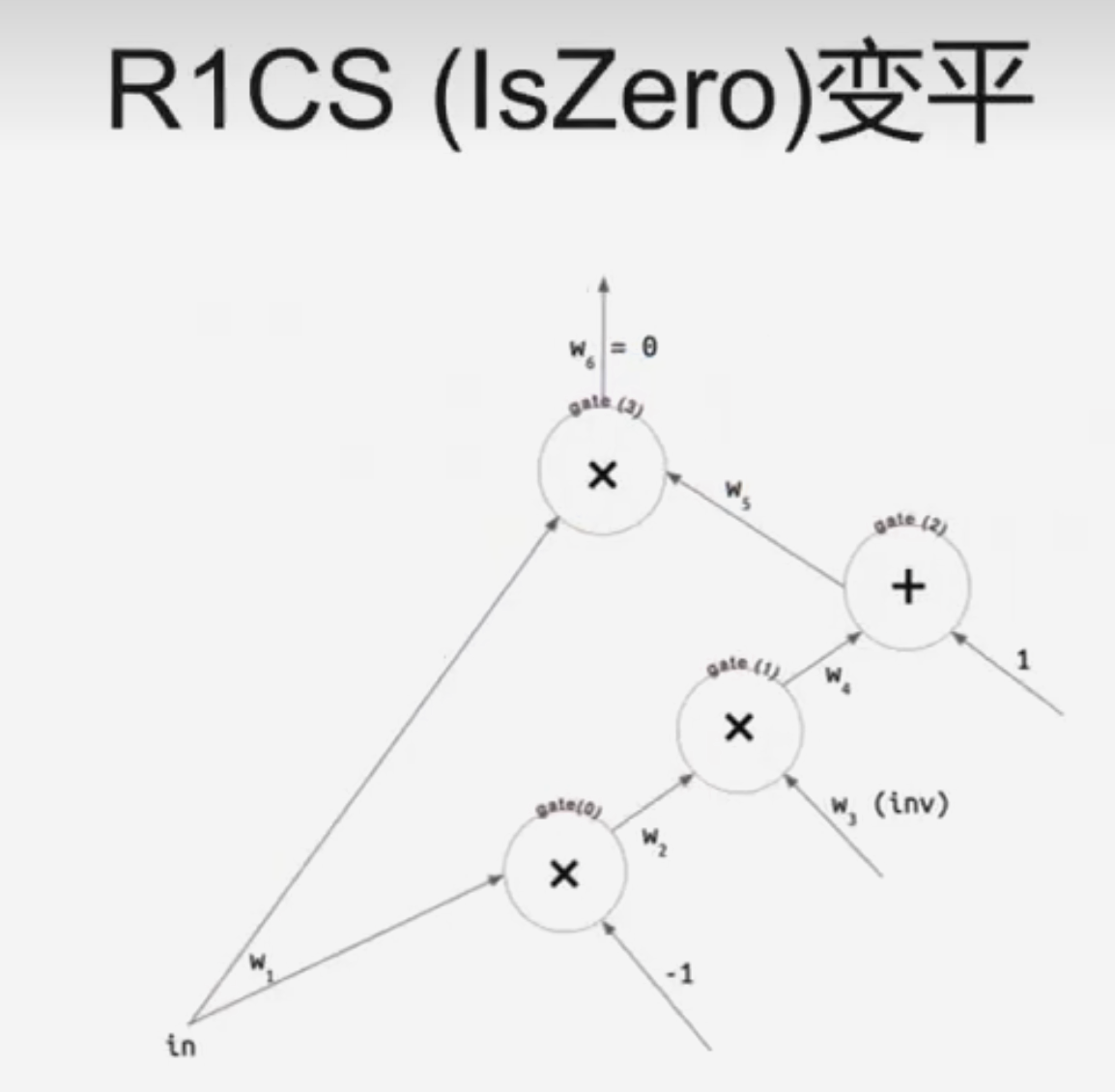
e.g. 2

对于这样的电路，其 R1CS 如下：

QAP

定义

QAP 是 R1CS 的多项式表示，它将一组向量点积约束转化为一个关于多项式的等式

$A(x) \cdot B(x) - C(x) = t(x) \cdot h(x)$

• 目标多项式 $t(x)$：

• • 这是一个公开的、非零的多项式。
• • 它的根（即 $t(x) = 0$ 的解）对应于原始电路中的每一个约束（例如，每一个乘法门或加法门）。
• • 如果有 m 个约束，通常选择 m 个不同的点（如 x = 1, 2, ..., m）作为 t(x) 的根，因此 t(x) = (x-1)(x-2)...(x-m)。

• 多项式 $A(x)$, $B(x)$, $C(x)$：

• • 假设有 n 个变量（包括输入、输出和中间变量），那么 A(x) 是一个长度为 n 的向量，A(x) = [A₁(x), A₂(x), ..., Aₙ(x)]，每个 Aᵢ(x) 都是一个多项式。
• • B(x) 和 C(x) 的结构类似。
• • 这些多项式是通过对 R1CS 中的向量进行插值得到的

• 商多项式 $h(x)$：

• • 这是一个辅助多项式，其存在性是验证的关键

补充：拉格朗日插值

拉格朗日插值的基本概念

拉格朗日插值是一种通过已知的数据点构造多项式的方法。给定 n+1 个不同的点 $(x_0, y_0), (x_1, y_1), ..., (x_n, y_n)$，拉格朗日插值公式可以构造一个次数不超过 n 的多项式 $P(x)$，使得 $P(x_i) = y_i$。

拉格朗日插值多项式的公式为：

$P(x) = \sum_{i=0}^{n} y_i \cdot L_i(x)$

其中 $L_i(x)$ 是拉格朗日基多项式：

$L_i(x) = \prod_{j=0, j \neq i}^{n} \frac{x - x_j}{x_i - x_j}$

在 QAP 中的作用

1. 从 R1CS 向量到多项式的转换

   • 在 R1CS 中，每个约束对应一组向量 $a, b, c$
   • 假设有 m 个约束，我们选择 m 个不同的求值点（通常是 $x = 1, 2, ..., m$）
   • 对于第 i 个变量，我们有 m 个值：$a_i^1, a_i^2, ..., a_i^m$（分别对应 m 个约束中的系数）
   • 使用拉格朗日插值，我们可以构造多项式 $A_i(x)$，使得 $A_i(j) = a_i^j$

2. 具体构造过程

   对于变量 $i$：

   • 数据点：$(1, a_i^1), (2, a_i^2), ..., (m, a_i^m)$
   • 构造 A_i(x) = Σ_{j=1}^m a_i^j · L_j(x)
   • 其中 L_j(x) = Π_{k=1,k≠j}^m (x-k)/(j-k)

3. 验证的核心机制

   • 如果原始 R1CS 约束在所有求值点都成立，那么多项式等式 $A(x) \cdot B(x) - C(x)$ 在这些点处的值都为 0
   • 由于目标多项式 $t(x) = (x-1)(x-2)...(x-m)$ 在这些点处也为 0
   • 根据多项式的性质，$A(x) \cdot B(x) - C(x)$ 必须被 $t(x)$ 整除
   • 因此存在商多项式 $h(x)$，使得 $A(x) \cdot B(x) - C(x) = t(x) \cdot h(x)$

4. 安全性保证

   • 如果证明者试图作弊（即不满足原始约束），那么 $A(x) \cdot B(x) - C(x)$ 在某些求值点处不为 0
   • 这意味着该多项式不能被 $t(x)$ 整除，无法找到有效的 $h(x)$
   • 拉格朗日插值确保了这种"点约束"到"多项式约束"的等价转换

示例 假设有 3 个约束，选择求值点 $x = 1, 2, 3$：

• 对于变量 1：在约束 1 中系数为 2，在约束 2 中系数为 5，在约束 3 中系数为 1
• 构造 $A_1(x)$ 使得 $A_1(1) = 2, A_1(2) = 5, A_1(3) = 1$

计算拉格朗日基多项式：

• $L_1(x) = \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} = \frac{(x-2)(x-3)}{(1-2)(1-3)} = \frac{(x-2)(x-3)}{2}$
• $L_2(x) = \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} = \frac{(x-1)(x-3)}{(2-1)(2-3)} = \frac{(x-1)(x-3)}{-1} = -(x-1)(x-3)$
• $L_3(x) = \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} = \frac{(x-1)(x-2)}{(3-1)(3-2)} = \frac{(x-1)(x-2)}{2}$

构造插值多项式：

$A_1(x) = 2 \cdot L_1(x) + 5 \cdot L_2(x) + 1 \cdot L_3(x)$

$= 2 \cdot \frac{(x-2)(x-3)}{2} + 5 \cdot (-(x-1)(x-3)) + 1 \cdot \frac{(x-1)(x-2)}{2}$

$= (x-2)(x-3) - 5(x-1)(x-3) + \frac{(x-1)(x-2)}{2}$

展开计算：

• $(x-2)(x-3) = x^2 - 5x + 6$
• $-5(x-1)(x-3) = -5(x^2 - 4x + 3) = -5x^2 + 20x - 15$
• $\frac{(x-1)(x-2)}{2} = \frac{x^2 - 3x + 2}{2} = 0.5x^2 - 1.5x + 1$

最终结果：

$A_1(x) = (x^2 - 5x + 6) + (-5x^2 + 20x - 15) + (0.5x^2 - 1.5x + 1)$

$= -3.5x^2 + 13.5x - 8$

验证：

• $A_1(1) = -3.5(1) + 13.5(1) - 8 = 2$ ✓
• $A_1(2) = -3.5(4) + 13.5(2) - 8 = -14 + 27 - 8 = 5$ ✓
• $A_1(3) = -3.5(9) + 13.5(3) - 8 = -31.5 + 40.5 - 8 = 1$ ✓

QAP的作用

1. 为密码学验证提供基础

• 多项式等式 $A(x) \cdot B(x) - C(x) = t(x) \cdot h(x)$ 可以通过椭圆曲线配对（Bilinear Pairing）进行高效验证

• 验证者不需要知道 $s$ 或 $w$，只需检查配对等式：

  $e([A(s)]_1, [B(s)]_1) = e([C(s)]_1, [G_2]) + e([t(s)]_2, [h(s)]_1)$

  （这里的 $[\cdot]_1, [\cdot]_2$ 表示在不同椭圆曲线群上的点，$e$ 是配对函数）

• 配对的双线性性质使得这个验证成为可能

2. 实现简洁性（Succinctness）

• 无论原始计算多么复杂（涉及成千上万个门），证明的大小和验证时间都只与多项式的次数有关，通常是常数或对数级别
• 验证者只需进行几次配对运算，即可验证整个计算的正确性

3. 支持零知识

• 证明者可以对多项式在秘密点 $s$ 的值进行"承诺"（如椭圆曲线上的点），而无需透露 $w$ 的具体值
• 通过随机化等技术，可以确保验证者无法从证明中获取关于 $w$ 的任何信息（除了它满足约束）

4. 连接算术化与密码学

• QAP 是从"计算 → R1CS → QAP → 密码学证明"这一链条中的关键一环
• 它将离散的向量约束"平滑"成了连续的多项式关系，为应用高级密码学工具（如配对）铺平了道路

步骤及示例

示例：验证 x³ + x + 5 = 35

步骤 1：构建 R1CS

首先将计算分解为基本约束：

• 约束 1：x * x = v1 （计算 x²）
• 约束 2：v1 * x = v2 （计算 x³）
• 约束 3：v2 + x = v3 （计算 x³ + x）
• 约束 4：v3 + 5 = 35 （加常数）

定义变量向量：w = [1, x, v1, v2, v3, 35] 假设 x = 3 是解，那么 w = [1, 3, 9, 27, 30, 35]

构建 R1CS 矩阵（每行对应一个约束）：

左矩阵 A：

    1  x  v1 v2 v3 35
C1 [0, 1, 0, 0, 0, 0]  // x
C2 [0, 0, 1, 0, 0, 0]  // v1
C3 [0, 1, 0, 1, 0, 0]  // v2 + x (线性化为 (v2 + x) * 1)
C4 [5, 0, 0, 0, 1, 0]  // v3 + 5

右矩阵 B：

    1  x  v1 v2 v3 35
C1 [0, 1, 0, 0, 0, 0]  // x
C2 [0, 1, 0, 0, 0, 0]  // x
C3 [1, 0, 0, 0, 0, 0]  // 1
C4 [1, 0, 0, 0, 0, 0]  // 1

输出矩阵 C：

    1  x  v1 v2 v3 35
C1 [0, 0, 1, 0, 0, 0]  // v1 = x*x = x^2
C2 [0, 0, 0, 1, 0, 0]  // v2 = v1*x = x^3
C3 [0, 0, 0, 0, 1, 0]  // v3 = (v2 + x)*1 = x^3 + x
C4 [0, 0, 0, 0, 0, 1]  // 35 = (v3 + 5)*1 = x^3 + x + 5

步骤 2：选择求值点

选择 4 个不同的点：{1, 2, 3, 4}（对应 4 个约束） 目标多项式：t(x) = (x-1)(x-2)(x-3)(x-4) = x⁴ - 10x³ + 35x² - 50x + 24

步骤 3：插值构造多项式

以变量 x 为例（索引为 1），从矩阵 A 中提取第 2 列：[1, 0, 1, 0]

使用拉格朗日插值构造 A₁(x)：

• 在点 1 处值为 1
• 在点 2 处值为 0
• 在点 3 处值为 1
• 在点 4 处值为 0

拉格朗日基多项式：

• L₁(x) = (x-2)(x-3)(x-4)/((1-2)(1-3)(1-4)) = (x-2)(x-3)(x-4)/(-6)
• L₂(x) = (x-1)(x-3)(x-4)/((2-1)(2-3)(2-4)) = (x-1)(x-3)(x-4)/2
• L₃(x) = (x-1)(x-2)(x-4)/((3-1)(3-2)(3-4)) = (x-1)(x-2)(x-4)/(-2)
• L₄(x) = (x-1)(x-2)(x-3)/((4-1)(4-2)(4-3)) = (x-1)(x-2)(x-3)/6

因此：

A₁(x) = 1·L₁(x) + 0·L₂(x) + 1·L₃(x) + 0·L₄(x)
      = L₁(x) + L₃(x)
      = -(x-2)(x-3)(x-4)/6 - (x-1)(x-2)(x-4)/2

类似地构造所有其他多项式 A₀(x), A₂(x), ... 和 B₀(x), B₁(x), ... 以及 C₀(x), C₁(x), ...

步骤 4：验证 QAP 关系

构造见证多项式：

A(x) = Σᵢ wᵢ · Aᵢ(x) = 1·A₀(x) + 3·A₁(x) + 9·A₂(x) + 27·A₃(x) + 30·A₄(x) + 35·A₅(x)
B(x) = Σᵢ wᵢ · Bᵢ(x) = 1·B₀(x) + 3·B₁(x) + 9·B₂(x) + 27·B₃(x) + 30·B₄(x) + 35·B₅(x)  
C(x) = Σᵢ wᵢ · Cᵢ(x) = 1·C₀(x) + 3·C₁(x) + 9·C₂(x) + 27·C₃(x) + 30·C₄(x) + 35·C₅(x)

如果见证正确，则在所有求值点 {1, 2, 3, 4} 处都有： A(i) · B(i) = C(i)

这意味着多项式 P(x) = A(x)·B(x) - C(x) 在这些点处都为 0，因此： P(x) = t(x) · h(x)

其中 h(x) 是商多项式，可以通过多项式长除法计算得出。

e.g.

补充材料