线性分析

第一部分：基础概念与核心思想

1.1 线性密码分析是什么？

• 定义：一种已知明文攻击（Known Plaintext Attack），由 Mitsuru Matsui 在1993年提出，首次成功攻破了 DES。
• 目标：通过分析大量明文-密文对 (P, C)，找到关于明文比特、密文比特和密钥比特之间的一个高概率线性近似关系，并利用这个关系来恢复部分或全部密钥。
• 核心思想：如果一个密码算法是“完美”的，那么任意明文比特、密文比特和密钥比特的异或组合结果为0或1的概率都应该是精确的 1/2。线性分析就是要找出那些概率显著偏离 1/2 的线性关系。

1.2 线性近似关系的数学表达

• 基本形式：$$P[i_0]\oplus P[i_1]\oplus \cdots \oplus C[j_0]\oplus C[j_1]\oplus \cdots =K[{\ell }_0]\oplus K[{\ell }_1]\oplus \cdots$$
  • P[i] 表示明文的第 i 位。
  • C[j] 表示密文的第 j 位。
  • K[ℓ] 表示密钥的第 ℓ 位。
• 更优雅的表示法（使用内积/掩码）：$$\alpha \cdot P\oplus \beta \cdot C=\gamma \cdot K$$
  • α, β, γ 是线性掩码（Linear Masks），它们是二进制向量。
  • α · P 表示向量 α 和 P 的点积（即对应位相乘再异或，等价于 α 中为1的位置对应的 P 的比特的异或）。
  • 这个公式简洁地描述了“选中哪些明文、密文、密钥比特进行异或”。

1.3 衡量近似关系质量的关键指标

• 概率(p)：上述线性关系成立（左边等于右边）的概率。
• 偏差(Bias, ε)：这是最核心的指标，衡量概率 p 偏离理想值 1/2 的程度。$$\epsilon =p-\frac{1}{2}$$
  • 如果 ε = 0，说明这个关系是随机的，没有用。
  • 如果 |ε| 越大，说明这个近似关系越“好”，越能用来区分密码算法和随机置换。
• 相关度(Correlation, c)：与偏差直接相关。$$c=2\epsilon$$
  • 相关度 c 的取值范围是 [-1, 1]。

---

第二部分：核心工具：S盒的线性分析

2.1 S盒（Substitution Box）是关键

• 分组密码（如DES, SPN）的非线性主要来源于S盒。因此，线性分析的第一步就是分析S盒的线性特性。

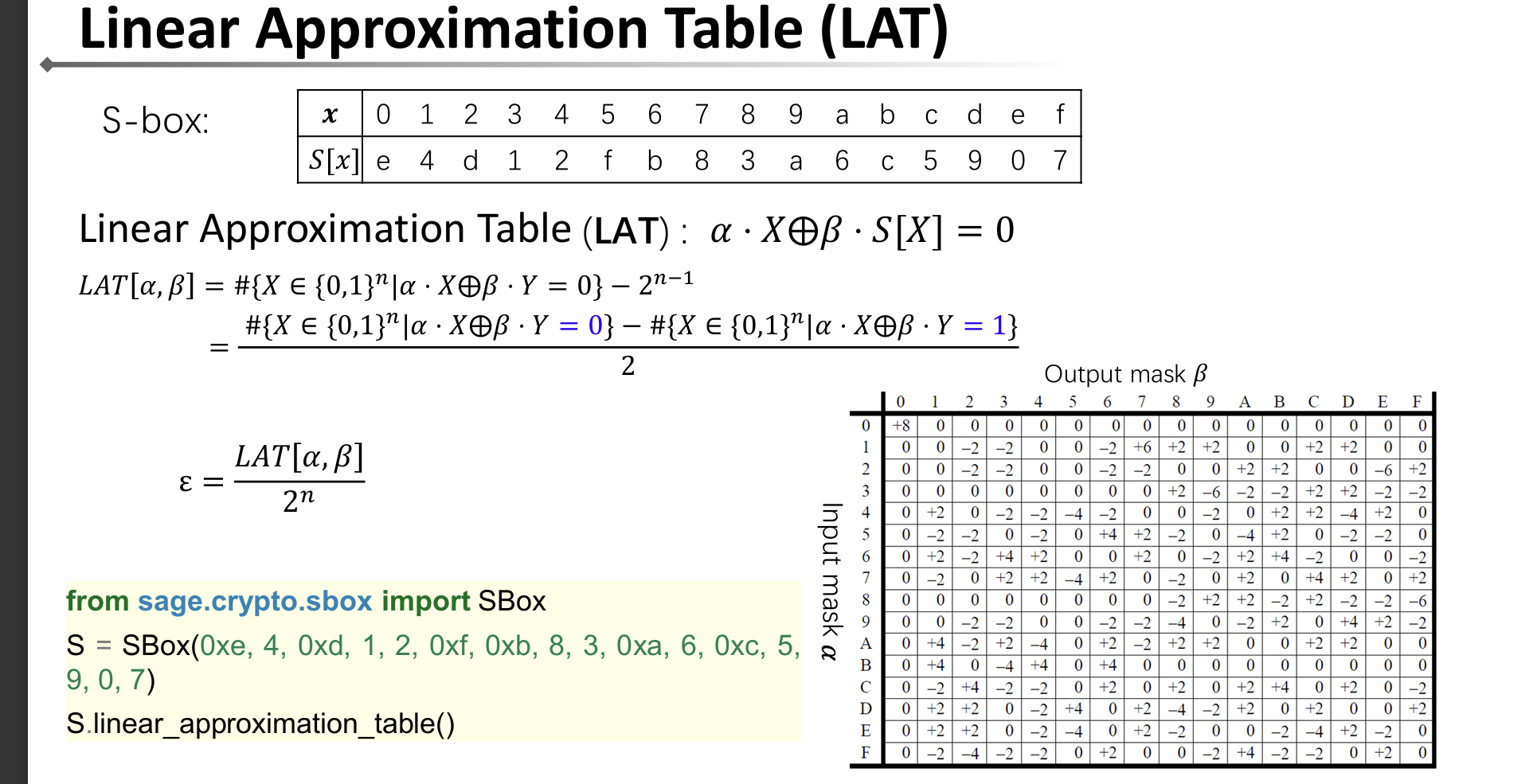
2.2 线性逼近表（LAT, Linear Approximation Table）

• 作用：LAT 是一个表格，它系统地记录了S盒所有可能的输入掩码 α 和输出掩码 β 组合下，线性近似 α·X ⊕ β·S(X) = 0 成立的次数。
• 构建方法：
  1. 对于每一个可能的输入掩码 α (0 到 2ⁿ-1)。
  2. 对于每一个可能的输出掩码 β (0 到 2ᵐ-1)。
  3. 遍历所有可能的输入 X (0 到 2ⁿ-1)。
  4. 计算 α·X ⊕ β·S(X)。
  5. 统计结果为 0 的次数，记为 T。
  6. LAT 表中的值通常存储为 T - 2^(n-1)，这个值正好等于 2^(n-1) * c = 2^n * ε。
• 如何解读 LAT：
  • LAT[α, β] = 0 → ε = 0，无用。
  • LAT[α, β] 的绝对值越大 → |ε| 越大 → 近似关系越好。

第三部分：从S盒到整个密码：线性特征（Linear Characteristic）

3.1 线性特征（Linear Trail）

• 定义：一条贯穿整个密码算法多轮的线性近似路径。它由一系列输入掩码和输出掩码组成，例如 α → β → γ → ...。
• 目标：找到一条从明文掩码 α 到密文掩码 β 的线性特征，使得其整体偏差 |ε| 尽可能大。

3.2 核心定理：Piling-Up Lemma（堆积引理）

• 作用：这是线性分析的基石，用于计算多轮（或多S盒）组合后的总偏差。
• 前提：假设各个随机变量（通常是各个S盒的输入/输出）是相互独立的。
• 结论：
  • 对于两个独立的随机变量 X₁ 和 X₂，其偏差分别为 ε₁ 和 ε₂。
  • 那么 Pr[X₁ ⊕ X₂ = 0] = 1/2 + 2ε₁ε₂。
  • 因此，X₁ ⊕ X₂ 的总偏差 ε_total = 2ε₁ε₂。
• 推广到 k 个变量：$${\epsilon }_{\text{total}}=2^{k-1}\prod _{i=1}^k{\epsilon }_i$$
• 重要推论：
  • 总相关度等于各部分相关度的乘积：c_total = c₁ * c₂ * ... * c_k。
  • 每经过一个有偏差的组件（如一个S盒），总偏差会急剧减小。因此，要找到有效的攻击，必须找到一条每一轮偏差都尽可能大的路径。

3.3 线性映射（如P置换、密钥加）的处理

• 线性变换（如P置换）：对于一个线性函数 Y = L(X)，其良好的线性近似 (α, β) 满足 α = L^T(β)，其中 L^T 是 L 的转置矩阵。此时相关度 |c| = 1。
• 密钥加（XOR with Key）：这是一个仿射变换。它不会改变偏差的绝对值 |ε|，但可能会改变符号（即关系是等于 γ·K 还是等于 γ·K ⊕ 1）。

---

第四部分：密钥恢复：Matsui 的两种算法

一旦找到了一个高概率的线性特征 α·P ⊕ β·C = γ·K，就可以用它来恢复密钥 γ·K（即密钥的某些比特的异或值）。

4.1 Matsui's Algorithm 1（恢复1比特密钥信息）

• 适用场景：当线性特征可以直接关联到密钥的某个线性组合（如 γ·K）时。
• 步骤：
  1. 初始化两个计数器 T₀ = 0 和 T₁ = 0。
  2. 对于每一个已知的明文-密文对 (P, C)：
     • 计算 s = α·P ⊕ β·C。
     • 如果 s == 0，则 T₀++。
     • 如果 s == 1，则 T₁++。
  3. 判断：
     • 如果 T₀ > T₁，则猜测 γ·K = 0。
     • 如果 T₀ < T₁，则猜测 γ·K = 1。
• 所需数据量：大约 N ≈ 1 / ε² 个明文-密文对。偏差 |ε| 越小，需要的数据越多。

4.2 Matsui's Algorithm 2（恢复多比特密钥）

• 适用场景：当线性特征不能直接到达最后一轮的密钥，而是停在倒数第二轮的中间状态时（这是更常见的情况）。
• 核心思想：猜测最后一轮的部分密钥，然后用猜测的密钥去部分解密密文，得到倒数第二轮的输出，再用这个输出去验证线性特征。
• 步骤（以SPN密码为例）：
  1. 假设我们找到了一个很好的线性特征，它能预测到倒数第二轮的输出 W 的某些比特。
  2. 我们的目标是恢复最后一轮子密钥 k 的某些比特。
  3. 对每一个可能的 k 的猜测值：
     • 初始化计数器 T₀ = 0, T₁ = 0。
     • 对于每一个 (P, C)：
       • 用猜测的 k 部分解密 C，得到 W。
       • 计算 s = (α·P) ⊕ (β·W)。
       • 如果 s == 0，则 T₀++；否则 T₁++。
     • 计算差值 |T₀ - T₁|。
  4. 判断：那个使得 |T₀ - T₁| 最大的 k 的猜测值，极有可能就是正确的密钥。
• 复杂度：时间复杂度 = 数据量 N × 密钥猜测空间大小。这是一种区分器+穷举的结合。

---

第五部分：实例分析与总结

5.1 4轮SPN密码攻击流程

1. 分析S盒：找到S盒的最佳线性近似（如 x1,8 ⊕ x1,9 ⊕ x1,11 = y1,10，偏差为 ε_s）。
2. 构建线性特征：利用P置换的线性性质，将S盒的输出掩码传播到下一轮的输入掩码，形成一条贯穿4轮的路径。
3. 计算总偏差：使用 Piling-Up Lemma，将每一轮S盒的偏差相乘，得到整条特征的总偏差 ε_total。
4. 确定攻击点：该特征最终关联到第4轮输入（即第3轮输出）的某些比特。
5. 应用Algorithm 2：
   • 收集 N ≈ 1/ε_total² 个 (P, C) 对。
   • 猜测第4轮子密钥 k4 中与这些比特相关的8个蓝色比特。
   • 用猜测的 k4 解密 C 的对应S盒，得到第3轮输出 W 的对应比特。
   • 验证 α·P ⊕ β·W = 0 是否成立，并统计计数。
   • 找出使计数偏差最大的 k4 猜测值。

5.2 关键结论与设计启示

• 数据复杂度：由线性特征的总偏差 ε 决定，Data ≈ ε⁻²。
• 时间复杂度：对于Algorithm 2，Time ≈ Data × 2^{#guessed key bits}。
• 安全设计准则：
  • S盒设计：应使 LAT 中除平凡项（全0掩码）外的所有 |ε| 尽可能小（即满足“严格雪崩准则”）。
  • 扩散层设计（P置换）：应能快速将单个S盒的偏差扩散到多个S盒，使得多轮后总偏差 ε_total 迅速趋近于0。
• 历史意义：线性分析和差分分析是现代分组密码设计的两大基石性评估标准。任何新设计的密码都必须证明其能抵抗这两种攻击。

---

这份提纲涵盖了线性密码分析从基本概念、S盒分析、多轮特征构建到最终密钥恢复的完整链条，并解释了所有关键公式和算法。按照这个结构复习，你应该能够透彻理解这一重要的密码分析技术。