Appearance
MD结构的弱点与现代哈希函数设计
一、Merkle-Damgård (MD) 构造回顾
- 核心思想:通过一个压缩函数
F迭代处理消息块,将任意长输入压缩为固定长输出。 - 关键组件:
- 压缩函数
F:安全性的基石。 - 初始向量 (IV):固定的起始值。
- 填充规则:
消息 | 1 | 0...0 | 消息长度,确保后缀自由性。 - (可选)输出变换
D:如 MD5/SHA-1 中D是恒等变换。
- 压缩函数
二、MD结构的固有弱点
1. 消息扩展攻击 (Message Extension Attack)
- 场景:尝试用
H(K || M)直接构造 MAC(消息认证码)。 - 漏洞:已知
(M, Tag=H(K||M)),攻击者无需知道密钥K,即可计算Tag' = H(K || M || padding || M'),从而伪造对M || padding || M'的有效认证标签。 - 原因:MD结构的链式特性使得哈希值可以直接作为下一轮压缩函数的输入状态。
- 解决方案:使用 HMAC 等经过专门设计的 MAC 构造。
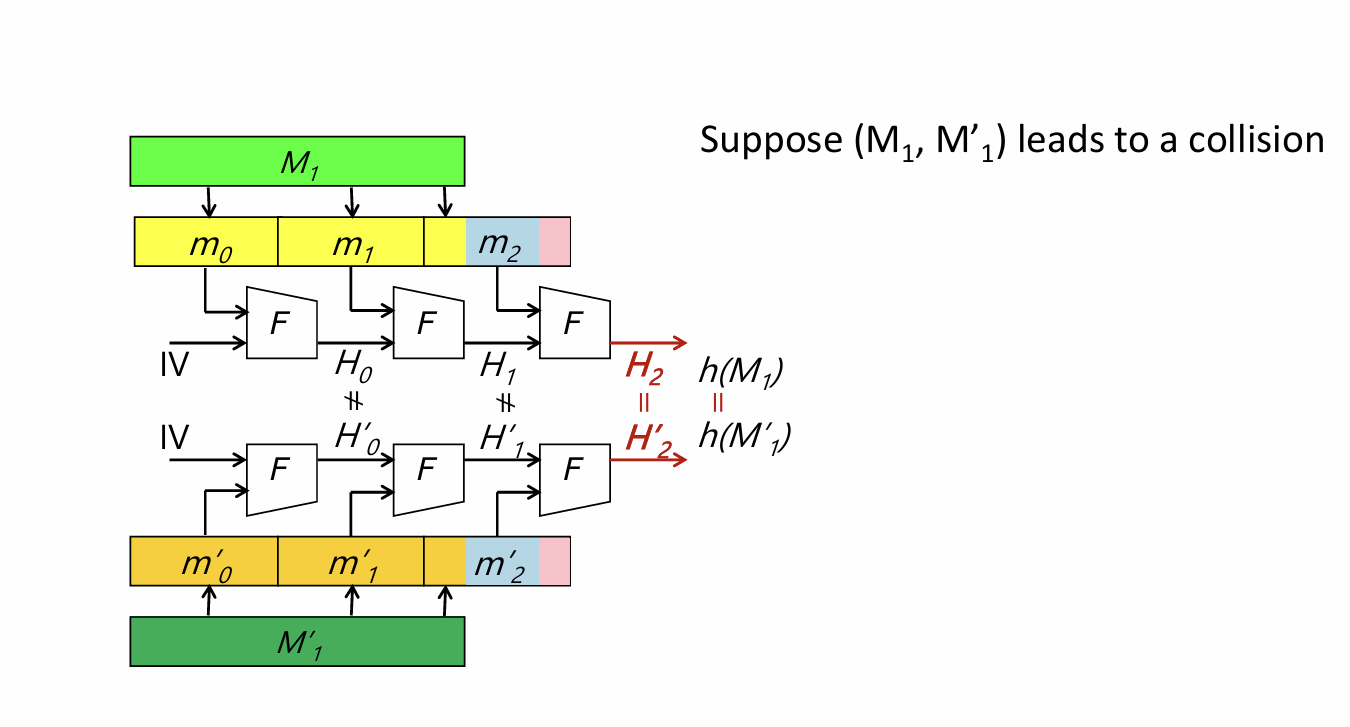
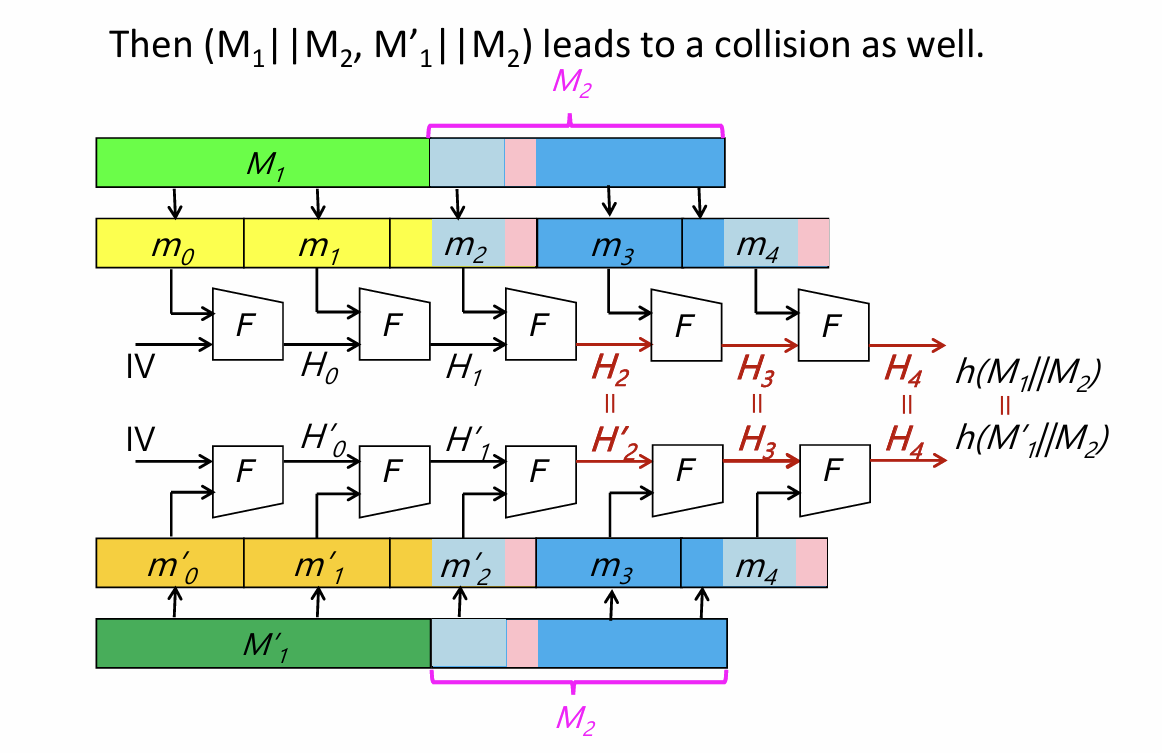
2. 多碰撞攻击 (Multi-collision Attack)
- 定义:找到
t个不同的消息,它们具有相同的哈希值。 - MD结构的脆弱性:
- 对于理想哈希函数,找
t-碰撞的复杂度约为。 - 但在MD结构中,利用生日攻击可以高效地构造
2^k-碰撞:- 找到第一对碰撞
(M1, M1*),得到中间状态H1。 - 以
H1为起点,找到第二对碰撞(M2, M2*),得到H2。 - 组合起来,
(M1|M2), (M1*|M2), (M1|M2*), (M1*|M2*)构成一个4-碰撞。
- 找到第一对碰撞
- 总复杂度:仅为
k * 2^{n/2},远低于理想情况。
- 对于理想哈希函数,找
- 影响:表明MD结构的多碰撞并不比普通碰撞更难找。
3. 长消息的第二原像攻击
场景A(无长度填充):
- 攻击思路:给定一个长目标消息
mtarget(含2^k块),攻击者可以:- 计算
mtarget所有前缀的中间哈希值(集合A)。 - 随机生成约
2^{n-k}个短消息,并计算它们从IV开始的哈希值(集合B)。 - 在A和B中寻找匹配点
Hi = Hj。 - 一旦找到,
Mj || m_{i+1} || ... || m_{2^k}就是mtarget的一个第二原像。
- 计算
- 复杂度:
O(2^{n-k}),对于长消息 (k大),远低于O(2^n)。
- 攻击思路:给定一个长目标消息
场景B(有长度填充):
- 攻击工具:可扩展消息 (Expandable Messages)。
- 原理:利用多碰撞技术,构造一组消息,它们都产生相同的中间哈希值,但长度各不相同(例如,能构造出长度从
k到k+2^k-1的消息)。 - 攻击流程:
- 为目标消息的前
k块生成一个(k, k+2^k-1)-可扩展消息集。 - 从第
k块的中间状态开始,随机生成消息并计算其哈希,尝试与目标消息从第k+1块开始的所有中间状态匹配。 - 一旦匹配成功,就从可扩展消息集中选择一个恰好能补足总长度的消息,从而构造出有效的第二原像。
- 为目标消息的前
- 结论:即使有长度填充,MD结构对长消息的第二原像攻击依然有效。
4. Herding Attack (Nostradamus Attack)
- 目标:先公布一个哈希值
y,之后再根据已知信息“定制”一个满足H(x)=y的消息x,制造“预言”假象。 - 攻击核心:钻石结构 (Diamond Structure)。
- 预计算阶段:
- 构建一个高度为
2^k的钻石结构。它是一个有向无环图,从2^k个不同的起点出发,通过精心选择的碰撞路径,最终汇聚到一个公共终点y。 - 公布
y作为“预言”的哈希值。
- 构建一个高度为
- 在线阶段:
- 当真实信息
P(如股市指数)已知后,攻击者将其与一个随机盐S'拼接,并计算f(IV, P||S')。 - 如果该值恰好等于钻石结构中的某个起点
d0j,则攻击成功。 - 跟随从
d0j到y的预设路径,即可构造出完整消息x = (P, S', M02, M11, ...),满足H(x)=y。
- 当真实信息
- 预计算阶段:
- 复杂度:通过平衡预计算和在线计算,总复杂度可降至约
O(2^{87})(对于128位哈希),远低于O(2^{128})。
三、克服MD弱点的新结构与对策
1. 核心问题诊断
- 根本原因:MD结构的内部状态大小与最终输出的哈希值大小相等(
n位)。这使得所有上述攻击成为可能。
2. 改进方案:增大内部状态
宽管道 (Wide Pipe):
- 内部状态大小 (
2n) 大于输出哈希值大小 (n)。 - 效果:直接提高了上述所有攻击的复杂度,使其达到理论安全界。
- 实例:BLAKE-256(内部状态512位,输出256位)。
- 内部状态大小 (
HAIFA 结构:
- 在压缩函数的输入中额外加入盐值 (salt) 和已处理的消息比特数 (#bits)。
- 优点:
- 自然支持加盐哈希,增强安全性。
- 使Herding等攻击失效,因为攻击者无法控制或预测
#bits参数。
- 实例:BLAKE, GOST。
3. 革命性新范式:海绵结构 (Sponge Construction)
- 核心组件:一个大的置换函数
f,作用于b = r + c位的状态。- 速率 (Rate)
r:每次吸收或挤出的数据块大小。 - 容量 (Capacity)
c:隐藏的内部状态部分,决定了安全性(安全界为O(2^{c/2}))。
- 速率 (Rate)
- 工作模式:
- 吸收 (Absorb):将输入消息分块,与状态的
r部分异或,然后应用置换f。 - 挤出 (Squeeze):从状态的
r部分输出哈希值,每输出一块就应用一次置换f。
- 吸收 (Absorb):将输入消息分块,与状态的
- 优势:
- 灵活性:通过调整
r和c,可在速度和安全性之间权衡。 - 多功能性:同一结构可用于哈希、MAC、流加密、认证加密等。
- 天然抗扩展:由于是置换而非压缩,不存在链式状态,因此可以直接安全地用于
H(K||M)形式的MAC。
- 灵活性:通过调整
- 标准实例:Keccak (SHA-3)。
📝 复习题与答案
题目 1:为什么在MD结构中,H(K || M) 不能直接用作安全的MAC?而海绵结构(如SHA-3)却可以?
答:
- MD结构的问题:源于其链式迭代特性。哈希值
H(K||M)本质上就是处理完K||M后的内部链变量。攻击者拿到(M, Tag)后,可以将Tag直接当作新的初始状态,继续处理任意附加数据M',从而计算出H(K || M || padding || M'),完成伪造。这就是消息扩展攻击。 - 海绵结构的优势:其内部状态 (
b = r + c位) 远大于 输出的哈希值 (r位)。当输出Tag时,攻击者只能看到r位,而关键的c位(容量)被隐藏了。没有完整的内部状态,攻击者无法继续“吸收”新的消息块M',因此消息扩展攻击失效。这使得Sponge(K || M)可以安全地用作MAC。
题目 2:简述多碰撞攻击如何利用MD结构的迭代特性来降低攻击复杂度。
答: 多碰撞攻击巧妙地利用了MD结构的模块化和状态继承特性。
- 分解问题:不是直接寻找
2^k个消息的碰撞,而是将其分解为k次独立的2-碰撞(即普通碰撞)查找。 - 状态接力:第一次找到的碰撞对
(M1, M1*)会产生一个共同的中间状态H1。这个H1被用作第二次碰撞查找的“新IV”。 - 组合爆炸:每找到一个新的碰撞对,可碰撞的消息数量就翻倍。经过
k次操作,就能组合出2^k个不同的消息,它们都导向同一个最终哈希值。 - 复杂度:总时间复杂度为
k次生日攻击的代价,即k * O(2^{n/2}),这比对理想哈希函数进行2^k-碰撞攻击的O(2^{n(k-1)/k})要低得多,尤其当k较大时。
题目 3:Herding Attack(Nostradamus Attack)的“钻石结构”是如何帮助攻击者实现“事后预言”的?
答: 钻石结构是Herding Attack成功的预计算基石,它解决了“先承诺后定制”的核心矛盾。
- 预计算(承诺阶段):攻击者预先构建一个钻石结构。这个结构有海量(
2^k个)不同的入口点,但所有路径最终都汇聚到唯一一个出口点y。然后,攻击者公开y,声称它是未来某个预言x的哈希值。 - 在线攻击(定制阶段):当真实的事件
P发生后,攻击者需要构造x使得H(x)=y。他将P与一个随机盐S'拼接,并计算其哈希的初始几步。如果结果碰巧等于钻石结构的某一个入口点d0j,那么攻击就成功了一半。 - 路径跟随:一旦匹配到入口点
d0j,攻击者只需简单地沿着预计算好的、从d0j到y的唯一路径,将路径上对应的块附加到(P, S')后面,就得到了完整的x。 - 效果:通过这种“广撒网”(大量入口)+“精跟踪”(唯一路径)的策略,攻击者能够以远低于暴力破解的复杂度,实现看似神奇的“预言”。