Plonk方案

Plonk全称为Permutations(排列) over Lagarange-bases(拉格朗日基) for Oecumenical(普世的) Noninteractive arguments of Knowledge。

准备阶段

准备双线性映射的两个群

这里建议先再看看之前的KZG承诺

定义有限域

• 这里使用$y^2=x^3+3$,既bls12_381曲线
• $x,y\in F_p$

以下以$x,y\in F_{101}$为例

寻找$G_1$的循环子群

下面的具体计算可以参考这里

扩展域

为了完成双线性映射需要找到扩展域 ${\mathbb{F}}_{101}$ ，这里的 $k$ 被称为嵌入度，需要找到最小的 $k$ 使得 $r|p^k-1$，在这里 $r$ 是子群 $G_1$ 的阶。要求 r | p^k − 1 是为了让 r 次单位根包含在 F_{p^k}^× 中，从而配对 e: G1 × G2 → GT（|GT|=r）可以定义。

在这里假设 $k-2$

• $p^k-1={101}^2-1\equiv 0mod17$
• 扩展域 ${\mathbb{F}}_{{101}^2}$
• 寻找一个不可约多项式 $x^2+2$
• • 为什么不能用 $x^2+1$, $\because (x-10)(x+10)\equiv x^2-100\equiv x^2+1mod101$
• $u$ 为该式的解，既 $u^2=-2$
• 则在该扩展域上所有元素可写作$ a + bu $

找到第二个子群

可信设置

• 生成私钥 $s,\alpha \in {\mathbb{F}}_p$
• 构造结构引用字符串SRS：
• • $1\cdot G_1,s\cdot G_1,s^2\cdot G_1,\cdots ,s^{n+2}\cdot G_1$
• • $1\cdot G_2,s\cdot G_2$

将问题转化为电路

这里将问题假设为： ${\alpha }^2+{\beta }^2={\gamma }^2$

我们要证明我们有 $\alpha =3,\beta =4,\gamma =5$ 满足上述等式。

R1CS:

• $x_1\cdot x_1=x_2$
• $x_3\cdot x_3=x_4$
• $x_5\cdot x_5=x_6$
• $x_2+x_4=x_6$

Plonk基本多项式

$$q_{l}a+q_{r}b+q_{o}c+q_{m}ab+q_c=0$$

• $q_l$：左输入
• $q_r$：右输入
• $q_o$：输出
• $q_m$：乘法
• $q_c$：常数

$q_{\ast }$表示为当前功能是否启用，启用为1，禁用为0，具体如下图：

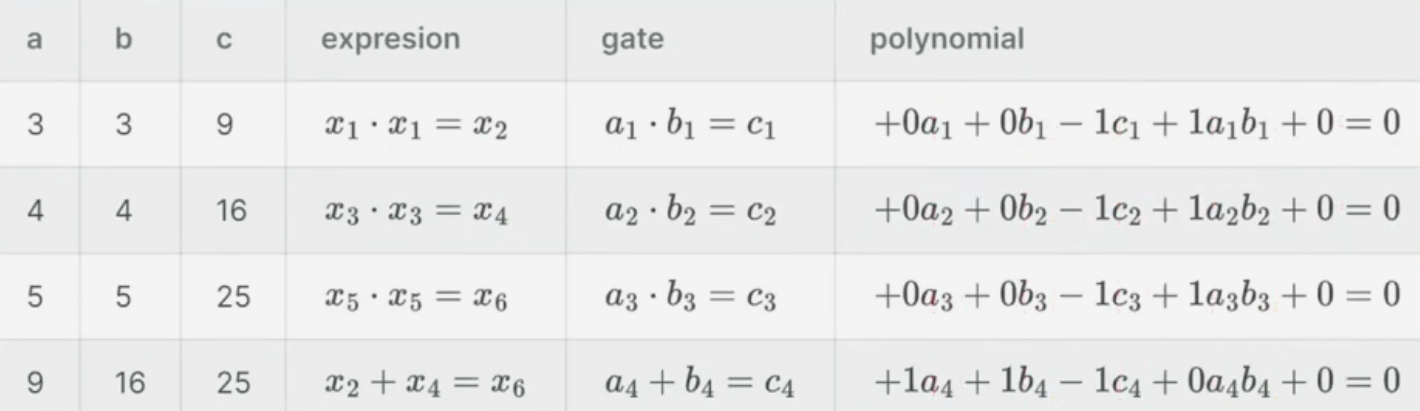
转化为向量：

拉格朗日插值，把向量转为多项式

这里对 $a=(3_0,4_1,5_2,9_3)$ 进行插值，转换为坐标则为 $(0,3),(1,4),(2,5),(3,9)$，最终得到多项式 $\frac{1}{2}{x}^3-\frac{3}{2}{x}^2+2x+3$，

具体参照之前的介绍

单位根

定义：对$x^n=1$ ，在复数意义的解下是 $n$ 次复根，这样的解有 $n$ 个，则称为$n$次单位根或单位复根，$n$ 要大于等于约束向量的长度。

在当前的例子中向量长度为4。

寻找单位根

在上面这里提到 $ind(G_1)=17$，则显然 ${\mathbb{F}}_{17}\in {\mathbb{F}}_{101}$，可以在 ${\mathbb{F}}_{17}$ 中寻找单位根:

计算陪集

对于上面的单位根 $H$ 在 ${\mathbb{F}}_{17}$ 中，有如下元素不重复的陪集：

$$k_1=2,k_{1}H=\{2,8,15,9\}$$$$k_2=3,k_{2}H=\{3,12,14,5\}$$

拷贝约束

由于需要构建 $x_{\ast }\mathrm{到}{a}_{\ast },b_{\ast },c_{\ast }$ 的映射关系，这里需要添加拷贝约束:

还需要嵌入到多项式中：

具体看Code

承诺

为了简化表示，以下用 $[a{]}_1$ 表示 $a{G}_1$，角标省略默认为 $G_1$，对于双线性配对容易得到分配率：

$$([a{]}_1+[b{]}_1)\cdot [c{]}_2=[a{]}_1\cdot [c{]}_2+[b{]}_1\cdot [c{]}_2$$

Stage 1 ：承诺a，b，c

对于在单位根中的群 $Z_H(x)=x^4-1$，我们有：

$\begin{array}{r}a(x)=(b_{1}x+b_2)\cdot Z_H(x)+f_a(x)\\ b(x)=(b_{3}x+b_4)\cdot Z_H(x)+f_b(x)\\ c(x)=(b_{5}x+b_6)\cdot Z_H(x)+f_c(x)\end{array}$

在 ${\mathbb{F}}_{1}7$ 上产生随机数：

$$(b_1,b_2,b_3,b_4,b_5,b_6)=(7,4,11,12,16,2)$$

易得：

$\begin{array}{rl}& a(x)=14+6x+3x^2+3x^3+4x^4+7x^5\\ & b(x)=12+9x+14x^2+13x^3+12x^4+11x^5\\ & c(x)=4+6x+11x^2+4x^3+2x^4+16x^5\end{array}$

然后使用SRS进行承诺：

取 $x=s$

$$[a(x)]=[a(x)]\cdot (1,2)=(91,66)$$$$[b(x)]=(26,45)$$$$[c(x)]=(91,35)$$

这里是和基点 $G_1=(1,2)$ 相乘

Sage 2 : 承诺 $z(x)$

产生随机数：$(b_7,b_8,b_9)=(14,11,7)\in {\mathbb{F}}_{17}$

获得挑战：$(\beta ,\gamma )=(12,13)\in {\mathbb{F}}_{17}$

计算 $z(x)$：

$$z(x)=(b_7{x}^2+b_{8}x+b_9)\cdot Z_H(x)+acc(x)$$$$ac{c}_0=1$$$$ac{c}_i=ac{c}_{i-1}\frac{(a_i+\beta {\omega }^{i-1}+\gamma )(b_i+\beta k_1{\omega }^{i-1}+\gamma )(c_i+\beta k_2{\omega }^{i-1}+\gamma )}{(a_i+\beta S_{{\sigma }_1}({\omega }^{i-1})+\gamma )(b_i+\beta S_{{\sigma }_2}({\omega }^{i-1})+\gamma )(c_i+\beta S_{{\sigma }_3}({\omega }^{i-1})+\gamma )}$$$$ac{c}_1=1\cdot \frac{(3+12\ast 1+13)(3+12\ast 2\ast 1+13)(9+12\ast 3\ast 1+13)}{(3+12\ast 2+13)(3+12\ast 1+13)(9+12\ast 13+13)}=\frac{11\cdot 6\cdot 7}{6\cdot 11\cdot 8}=3$$$$ac{c}_2=3\cdot \frac{(4+12\ast 4+13)(4+12\ast 2\ast 4+13)(16+12\ast 3\ast 4+13)}{(4+12\ast 8+13)(4+12\ast 4+13)(16+12\ast 9+13)}=3\cdot \frac{14\cdot 11\cdot 3}{11\cdot 14\cdot 1}=9$$$$ac{c}_2=9\frac{(5+12\ast 16+13)(5+12\ast 2\ast 16+13)(25+12\ast 3\ast 16+13)}{(5+12\ast 15+13)(5+12\ast 16+13)(25+12\ast 5+13)}=9\cdot \frac{6\cdot 11\cdot 2}{11\cdot 6\cdot 13}=4$$$$acc(x)=16x+5x^2+14x^3$$$$z(x)=(14x^2+11x+7)(x^4-1)+16x+5x^2+14x^3=10+5x+8x^2+14x^3+7x^4+11x^5+14x^6$$$$[z(x){]}_1=[z(x)]\ast (1,2)=(32,59)$$

Stage 3 : 计算商多项式 $q(\alpha )$ 与承诺 $t$

$\alpha =15\in {\mathbb{F}}_{17}$

$t(x)=(a(x)b(x)q_M(x)+a(x)q_L(x)+b(x)q_R(x)+c(x)q_O(x)+PI(x)+q_C(x))\frac{1}{Z_H(x)}$$+(a(x)+\beta x+\gamma )(b(x)+\beta k_{1}x+\gamma )(c(x)+\beta k_{2}x+\gamma )z(x)\frac{\alpha }{Z_H(x)}$$-(a(x)+\beta S_{{\sigma }_1}(x)+\gamma )(b(x)+\beta S_{{\sigma }_2}(x)+\gamma )(c(x)+\beta S_{{\sigma }_2}(x)+\gamma )z(\omega x)\frac{\alpha }{Z_H(x)}$$+(z(x)-1)L_1(x)\frac{{\alpha }^2}{Z_H(x)}$

然后将多项式分割为$degree<n+2$的多项式 $t_{lo}(x),t_{mid}(x),t_{hi}(x)$，$n$ 是指电路门数量，或者说向量长度，在这里 $n=4$ 其中：

$$t(x)=t_{lo}(x)+t_{mid}(x)+t_{hi}(x)$$

然后输出 $[t_{lo}(x)],[t_{mid}(x)],[t_{hi}(x)]$，既将 $x=s$ 代入并承诺到 $G_1$ 上

我们有：

$t(x)=11x^{17}+7x^{16}+2x^{15}+16x^{14}+6\ast x^{13}+$$15x^{12}+x^{11}+10x^{10}+2x^9+x^8+8x^7+13x^6+13x^5+9x^3+13x^2+16x+11$

$t_{lo}=11+16x+13x^2+9x^3+13x^5$

$t_{mid}=13+8x+x^2+2x^3+10x^4+x^5$

$t_{hi}=15+6x+16x^2+2x^3+7x^4+11x^5$

然后得到 Commit:

$$[t_{lo}{]}_1=(12,32)$$$$[t_{mid}{]}_1=(26,45)$$$$[t_{hi}{]}_1=(91,66)$$

Stage 4 : 线性化，计算评估点 $\zeta$

$\zeta =5\in {\mathbb{F}}_{19}$

计算：

$\overline{a}=a(\zeta ),\overline{b}=b(\zeta ),\overline{c}=c(\zeta )$$\overline{S_{{\sigma }_1}}=S_{{\sigma }_1}(\zeta ),\overline{S_{{\sigma }_2}}=S_{{\sigma }_2}(\zeta )$$\overline{t}=t(\zeta )$$\overline{z_{\omega }}=z(\omega \zeta )$

计算 $r(x)$:

$r(x)=\overline{a}\overline{b}{q}_M(x)+\overline{a}{q}_L(x)+\overline{b}{q}_R(x)+\overline{c}{q}_O(x)+q_C(x)$$+\alpha (\overline{a}+\beta \zeta +\gamma )(\overline{b}+\beta k_1\zeta +\gamma )(\overline{c}+\beta k_2\zeta +\gamma )z(x)$$-\alpha (\overline{a}+\beta \overline{S_{{\sigma }_1}}+\gamma )(\overline{b}+\beta \overline{S_{{\sigma }_2}}+\gamma )\beta \overline{z_{\omega }}{S}_{{\sigma }_3}(x)$$+{\alpha }^{2}z(x)L_1(\zeta )$

然后计算 $[r(s){]}_1$:

 

The definition of $r(x)$ here is not same as in plonk paper, where we removed all the constant terms when we do linearization. This can save one verifier scalar multiplication.

最后计算线性评估点：$\overline{r}=r(\zeta )$，输出

$$\overline{a},\overline{b},\overline{c},\overline{S_{{\sigma }_1}},\overline{S_{{\sigma }_2}},\overline{z_{\omega }},\overline{t},\overline{r}$$

$\overline{a}=a(5)=15,\overline{b}=13,\overline{c}=5,\overline{S_{{\sigma }_1}}=1,$$\overline{S_{{\sigma }_2}}=12,\overline{t}=1,\overline{z_{\omega }}=15$$r(x)=16x+9x^2+13x^3+8x^4+15x^5+16x^6,$$\overline{r}=15$

Stage 5 : 计算公开多项式承诺

$$W_{\zeta }(x)=\begin{array}{c}\frac{1}{x-\zeta }\end{array}\cdot \left[\begin{array}{c}{t}_{lo}(x)+{\zeta }^{n+2}{t}_{mid}(x)+{\zeta }^{2n+4}{t}_{hi}(x)-\overline{t}\\ +v(r(x)-\overline{r})\\ +v^2(a(x)-\overline{a})\\ +v^3(b(x)-\overline{b})\\ +v^4(c(x)-\overline{c})\\ +v^5(S_{{\sigma }_1}(x)-\overline{S_{{\sigma }_1}})\\ +v^6(S_{{\sigma }_2}(x)-\overline{S_{{\sigma }_2}})\end{array}\right]$$$$W_{\zeta \omega }(x)=\frac{z(x)-\overline{z_{\omega }}}{x-\zeta \omega }$$

输出：$[W_{\zeta }(x){]}_1,[W_{\zeta \omega }(x){]}_1$

给定 $\zeta =5$，有：$[W_{\zeta }(x){]}_1=(91,35),[W_{\zeta \omega }(x){]}_1=(65,98)$

证据输出

$\pi =([a],[b],[c],[z],[t_{lo}],[t_{mid}],[t_{hi}],[W_{\zeta }],[W_{\zeta \omega }]$$\overline{a},\overline{b},\overline{c},\overline{S_{{\sigma }_1}},\overline{S_{{\sigma }_2}},\overline{z_{\omega }},\overline{r})$

$\pi =((91,66),(26,45),(91,35),(32,59),(12,32),(26,45),(91,66),$$(91,35),(65,98),15,13,5,1,12,15,15)$

总共16个元素，9个$G_1$上的点，7个${\mathbb{F}}_p$上的标量

验证

SRS预处理

$\begin{array}{rl}& [q_M]=(12,69)\\ & [q_L]=(32,42)\\ & [q_R]=(32,42)\\ & [q_O]=(1,99)\\ & [q_C]=\mathrm{\infty }\\ & [s_{{\sigma }_1}]=(68,74)\\ & [s_{{\sigma }_2}]=(65,3)\\ & [s_{{\sigma }_3}]=(18,49)\end{array}$

证明步骤

1. 检查：$[a],[b],[c],[z],[t_{lo}],[t_{mid}],[t_{hi}],[W_{\zeta }],[W_{\zeta \omega }]\in G_1$

2. 检查：$\overline{a},\overline{b},\overline{c},\overline{S_{{\sigma }_1}},\overline{S_{{\sigma }_2}},\overline{z_{\omega }},\overline{r}\in {\mathbb{F}}_{17}$

3. 检查：$w_{i\in [l]}\in {\mathbb{F}}_{17}$

4. 计算零多项式评估：$Z_H(\zeta )={\zeta }^n-1$

5. 计算：$L_1(\zeta )=\frac{{\zeta }^n-1}{n(\zeta -1)}$

6. 计算：$PI(\zeta )=\sum _{i\in [l]}{w}_i{L}_i(\zeta )$

7. 计算商多项式评估：$\overline{t}=\frac{\overline{r}+PI(\zeta )-(\overline{a}+\beta \overline{S_{{\sigma }_1}}+\gamma )(\overline{b}+\beta \overline{S_{{\sigma }_2}}+\gamma )(\overline{c}+\gamma )\alpha -L_1(\zeta ){\alpha }^2}{Z_H(\zeta )}$

8. 计算第一部分多项式承诺，先定义：$[D]=v[r(x)]+u[z]$，计算： $[D]=\overline{a}\overline{b}v[q_M]+\overline{a}v[q_L]+\overline{b}v[q_R]+\overline{c}v[q_O]+v[q_C]$$+((\overline{a}+\beta \zeta +\gamma )(\overline{b}+\beta k_1\zeta +\gamma )(\overline{c}+\beta k_2\zeta +\gamma )\alpha v+L_1(\zeta ){\alpha }^{2}v+u)[z]$$-(\overline{a}+\beta \overline{S_{{\sigma }_1}}+\gamma )(\overline{b}+\beta S_{{\sigma }_2}+\gamma )\alpha v\beta \overline{z_{\omega }}[S_{{\sigma }_3}]$

9. 计算完整批多项式承诺

$$[F]=[t_{lo}]+{\zeta }^{n+2}[t_{mid}]+{\zeta }^{2n+4}[t_{hi}]+[D]+v^2[a]+v^3[b]+v^4[c]+v^5[S_{{\sigma }_1}]+v^6[S_{{\sigma }_2}]$$

10. 计算群编码的批量评估 $[E]$：

$$[E]=(\overline{t}+v\overline{r}+v^2\overline{a}+v^3\overline{b}+v^4\overline{c}+v^5\overline{S_{{\sigma }_1}}+v^6\overline{S_{{\sigma }_2}}+u\overline{z_{\omega }})\cdot [1]$$

11. 验证所有的等式：

$$e([W_{\zeta }]+u[W_{\zeta \omega }],[s{]}_2)=e(\zeta [W_{\zeta }]+u\zeta \omega [W_{\zeta \omega }]+[F]-[E],[1{]}_2)$$

 

Let's check steps 9 − 11 for each of the polynomials. For example the terms with 𝑢.

$e(u\cdot s\cdot [W_{\zeta \omega }],1)\doteq e(u\zeta \omega [W_{\zeta \omega }]+u[z]-uz(\omega \zeta ),1)$

$e(u\cdot (s-\zeta \omega )[W_{\zeta \omega }],1)\doteq e(u(z(s)-z(\omega \zeta ),1)$$(s-\zeta \omega )\frac{z(s)-z(\zeta \omega )}{s-\zeta \omega }\doteq z(s)-z(\omega \zeta )$

Let's check $r(x)$,here we define $[W_{\zeta }]=\frac{v(r(s)-r(\zeta ))}{s-\zeta }$ for simplicity:

$e(s\cdot [W_{\zeta }],1)\doteq e(\zeta [W_{\zeta }]+v\cdot r(s)-v\overline{r},1)$$e((s-\zeta )\cdot \frac{v(r(s)-r(\zeta ))}{s-\zeta },1)\doteq e(v(r(s)-r(\zeta )),1)$

Let's check $t(x)$,here we define $[W_{\zeta }]=\frac{t_{lo}(s)+{\zeta }^{n+2}{t}_{mid}(s)+{\zeta }^{2n+4}{t}_{hi}(s)-t(\zeta )}{s-\zeta }$ for simplicity:

$e((s-\zeta )[W_{\zeta }],1)\doteq e([t_{lo}]+{\zeta }^{n+2}[t_{mid}]+{\zeta }^{2n+4}[t_{hi}]-\overline{t},1)$$e(t_{lo}(s)+{\zeta }^{n+2}{t}_{mid}(s)+{\zeta }^{2n+4}{t}_{hi}(s)-t(\zeta ),1)\doteq e(t_{lo}(s)+{\zeta }^{n+2}{t}_{mid}(s)+{\zeta }^{2n+4}{t}_{hi}(s)-t(\zeta ),1)$

The other terms are easy to check as well.

Code

Plonk-by-Hand