零知识证明

完美零知识证明

对于任何给定的验证者策略，存在一个模拟器，该模拟器可以在没有访问实际证明者的情况下生成一个会话记录（即交互过程的转录），这个会话记录与实际交互产生的记录是完全不可区分的。这意味着，即使验证者拥有无限的计算能力，也无法从交互过程中获取到任何额外的信息。传统基于公私钥非对称加密的不是完美零知识证明。

通用交互式零知识证明

零知识证明理想属性

• 完备性：如果所有人都诚实并且遵守规则，则一定可以正确运行。
• 可靠性*(知识可靠性)*：如果证明者不遵守规则则一定失败。
• 零知识性：验证者除了正确性之外，不能获得任何额外的信息。

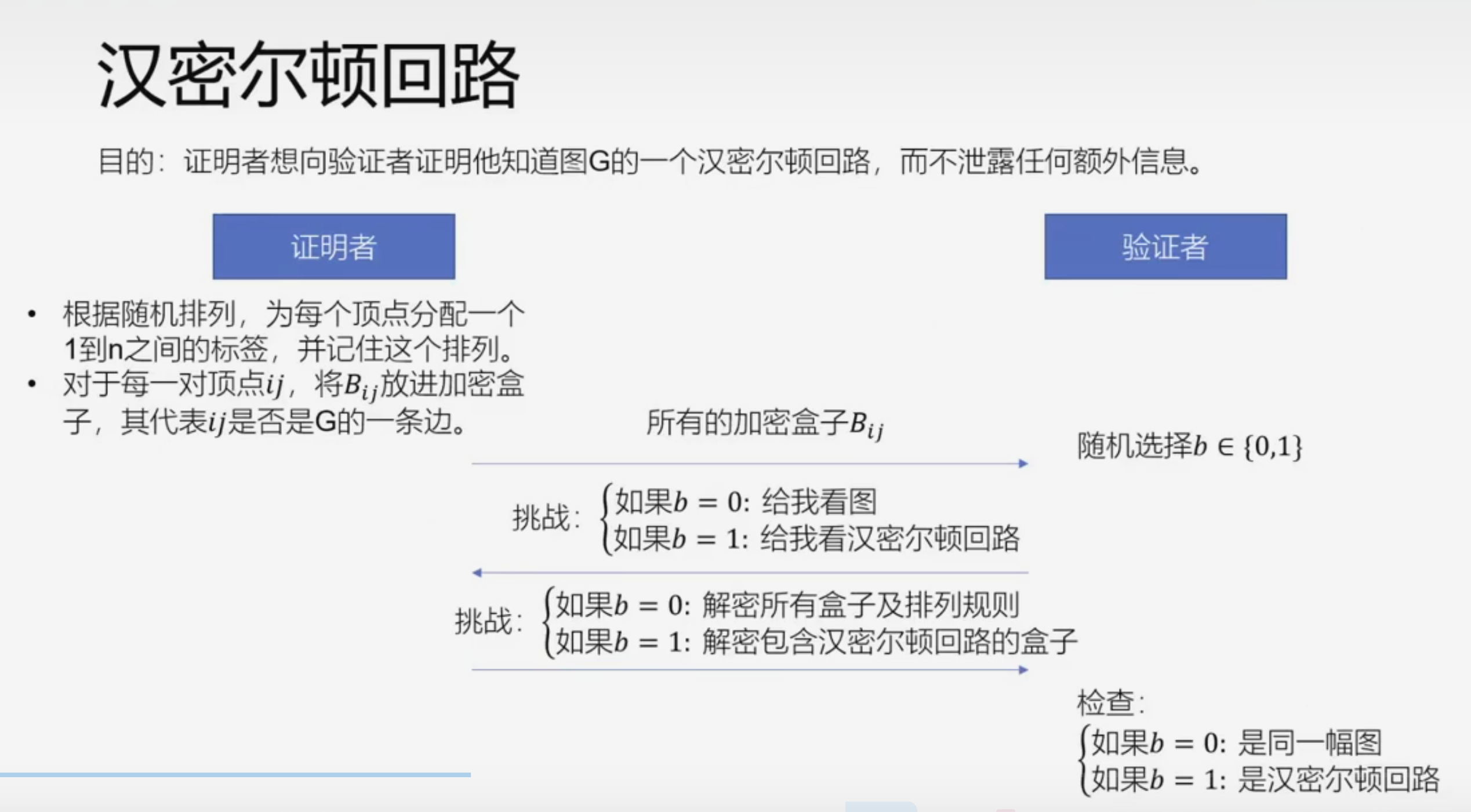
汉密尔顿回路

三色图问题

假设Alice有一张图，她想向Bob证明这张图是三色可着色的，但又不想泄露具体的着色方案，可以通过以下流程进行：

图同构问题

目标：证明两个图 G 和 H 是同构（存在双射 f 使得 f(G) = H），但不泄露具体的同构映射 f。

思路：证明者（Prover）利用随机置换把图打乱成一个中间图 G'，然后通过承诺-挑战-应答的方式证明 G' 与 G 或 H 中的某一个通过已知置换得到，从而在不暴露 f 的情况下说服验证者。

流程（图示）：

证明过程

 

如何证明“图无法三着色”

核心想法：把“三着色不可行”编码为 CNF F(G) 的不可满足性，并出一份可检验的不可满足证明（如 DRAT/FRAT）。然后使用通用零知识证明系统（zkSNARK/zkSTARK/Ligero/Spartan 等）证明“Check(F(G), π) = 1”，而不泄露证明 π 的具体内容。

• 步骤
  1. 约束编码：把 3-Coloring 编成 CNF F(G)（每个顶点选1色、每边两端不同色）。
  2. 生成证书：用 SAT 求解器对 F(G) 输出不可满足证明 π（DRAT/FRAT）。
  3. ZK 证明：构造电路/程序 Check(F(G), π)（一个标准证明检查器），Prover 生成 ZK 证明，证明“存在 π 使得 Check=1”。
  4. Verifier 仅检查 ZK 证明有效，无需看到 π。

• 说明
  • 这是计算型零知识“论证”（argument）：在常见密码假设下安全；零知识性来自通用 ZK 系统，不泄露 π。
  • 也可用基于计数的交互证明（sum-check 证明 #3COL(G)=0），但实现复杂度更高，工程上多采用“UNSAT 证书 + 通用 ZK”。

---

如何证明“给定 f 不是同构”

把“f 不是同构”表述为存在一个反例（见证）：

• 类型A（非单射）：∃ u≠v, f(u)=f(v)；
• 类型B（不保邻接）：∃(u,v)，使得 E_G(u,v) ≠ E_H(f(u), f(v))。

由于 G、H、f 公开，验证这些条件是多项式时间；我们仅隐藏“哪个 (u,v) 违反”，故可用通用 ZK 证明“存在这样的 (u,v)”。

• 步骤
  1. 定义关系 R(G,H,f; w)：w=(u,v,flag)，满足
     • flag=0：u≠v 且 f(u)=f(v)；或
     • flag=1：E_G(u,v) ≠ E_H(f(u),f(v))。
  2. Prover 以 w 为见证，构造电路 C(G,H,f; w)=1。
  3. 生成对语句“∃w: C=1”的 ZK 证明，不泄露 w。

• 说明
  • 若仅需“非零知识”的证明确认，直接给出一个反例（例如某条边的邻接不保留）即可被瞬间验证。
  • 需要隐藏反例时，用通用 ZK 把 G、H 当作电路常量，(u,v) 作为私密见证输入即可。

在后面的章节中，我们知道zkp在实际应用中，往往是基于这样的情形：Alice拥有一个或多个私密值，她想向Bob证明这些变量满足某组约束，而不泄露这些私密值本身。

多项式承诺分类

KZG	FRI	IPA	DARKS
基于双线性对	基于哈希函数	基于离散对数	基于理想二次类群 $_?$
不抗量子	抗量子	不抗量子	不抗量子