Appearance
基于属性加密
基于身份IBE
- 特点: 和CA相比,没有配置证书链的繁琐
- 缺点: 私钥生成中心KGC掌握所有私钥
Boneh-Franklin IBE
- 选择双线性映射的两个群和映射、随机数、哈希函数:
- 主私钥:
为了简化表达,视作 ,这里假设
- 选择随机数
- 计算
- 选择随机数
- 计算
- 计算
方案流程
IBE-多对私钥 (BF-IBE2)
- 选择双线性映射的两个群和映射、随机数、哈希函数:
- 主私钥:
- 选择随机数
- 选择随机数
- 选择随机数
- 计算
- 选择随机数
这个方案不满足不可区分性
- 假设有
,以及对应密文 - 由于密文
中存在 , 已知 - 同时可根据
导出 - 故而可以构造:
来判断密文是发送给哪个 的
- 假设有
FIBE(Fuzzy IBE)
Fuzzy IBE 是基于属性的加密的一种特殊形式,用户的私钥和密文都与一组属性相关联。只有当用户的属性集合与密文的属性集合满足一定的重叠条件时,用户才能成功解密密文。
以下是基于 Sahai-Waters 方案的构造(阈值
- 选择双线性映射群
阶为素数 ,生成元 - 随机选择主密钥
- 对于属性全集
中的每个属性 ,选择随机数 ,计算 - 公开参数:
- 主私钥:
- 选择双线性映射群
- 输入用户属性集合
( ),可以简单理解为一个 vector<string> - 构造一个
次多项式 ,使得常数项 ,其余系数随机 - 对于每个属性
,计算私钥组件: 其中 将属性映射为 中的元素 - 私钥:
- 输入用户属性集合
- 输入目标属性集合
- 选择随机数
- 计算密文组件(对于每个
): - 计算加密密钥
- 使用
加密消息 (例如 ) - 密文:
- 输入目标属性集合
- 计算属性交集
- 如果
,解密失败 - 选择
的一个子集 ,使得 - 对于
,计算配对: - 利用拉格朗日插值系数
在 处恢复 : - 使用恢复的密钥
解密消息
- 计算属性交集
基于属性ABE
ABE(Attribute-Based Encryption, 基于属性加密)把“谁能解密”这件事从身份提升为属性与规则。
核心差异在“访问控制结构”放在哪一侧:
- CP-ABE(Ciphertext-Policy ABE):
- 密文绑定策略(Policy),用户密钥绑定属性集合(Attributes)。
- 直觉:发布者(加密者)说了算——“满足这个策略的人都能解密”。
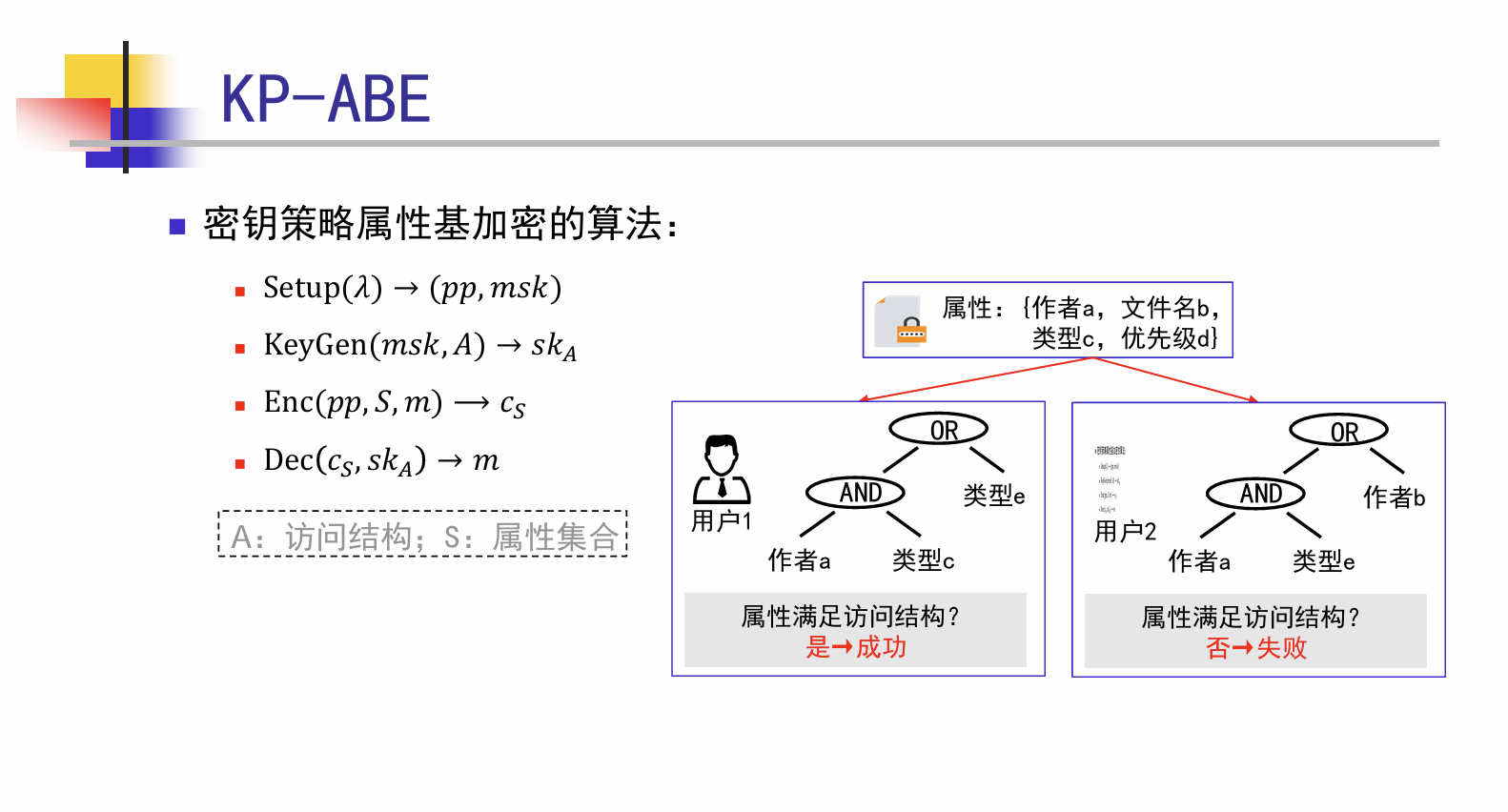
- KP-ABE(Key-Policy ABE):
- 密钥绑定策略(Policy),密文绑定属性集合(Attributes)。
- 直觉:发证方(KGC/AAA)说了算——“我给你的这把钥匙能打开哪些属性的密文”。

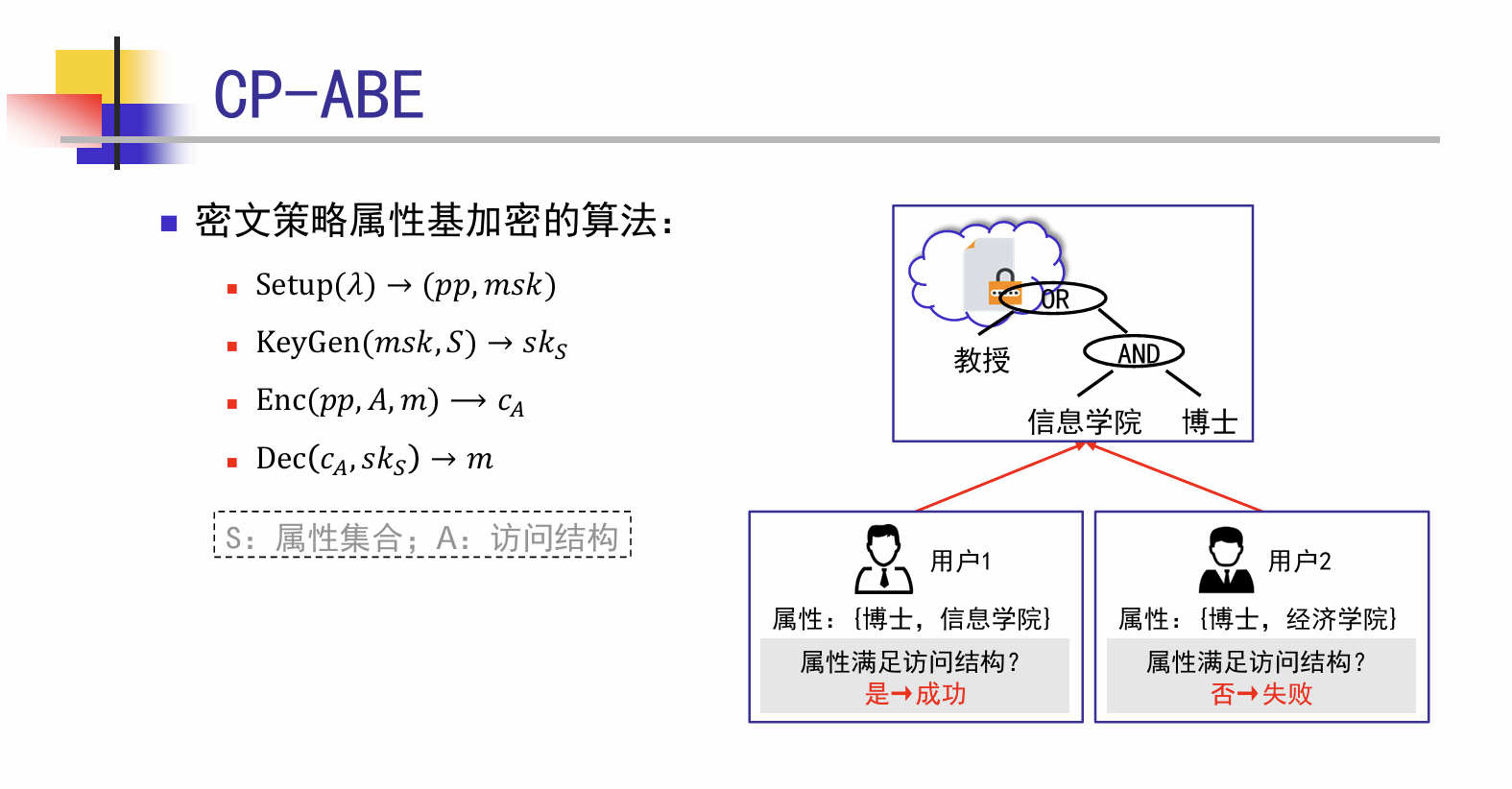
CP-ABE:密文侧策略树(PolicyTree)如何构建
1) “访问控制结构”长什么样?
CP-ABE 的访问控制结构通常用一棵阈值策略树来表示:
- 每个内部节点是一个 k-of-n 阈值门(至少满足
个子条件) - AND 门:
- OR 门:
- 一般阈值门:
- AND 门:
- 每个叶子节点绑定一个具体属性(例如
role:student) - 为了做阈值插值,子节点会有一个“位置编号”(可理解为 Shamir/Lagrange 插值里的
坐标)
你可以把策略树理解为一个“可计算的布尔/阈值表达式”,叶子节点是属性,内部节点表示“至少满足几个孩子”。
2) 用“组合”的方式搭策略树
CP-ABE 的关键是:加密时必须把完整策略带进密文。因此策略需要先被“结构化”为一棵树:
- 叶子 = 一个属性条件
- 内部节点 = 一个阈值门(k-of-n),其孩子是子条件
一个常见例子:
规则:
(role:student AND dept:cs) OR (role:teacher AND level>=2)
可以转成阈值门:
- 顶层 OR:
k=1, n=2 - 每个 AND:
k=2, n=2
对应结构(示意):
注意:这里的
level:>=2在代码里只是一个字符串属性。真实系统常见做法是把“范围/比较”改造成若干离散属性(比如level>=2、level>=3…),或者使用支持数值谓词的扩展方案。
3) CP-ABE 加密时策略树如何“落到密文里”?
加密算法会把“策略树”变成“密文里的结构化信息”,大致过程是:
- 随机挑
,作为根节点的秘密。 - 自顶向下用 Shamir secret sharing 在树上分发份额:对每个节点
得到一个份额 。 - 对每个叶子节点(属性
)生成密文组件(把“份额”绑定到该属性上): - 用
派生对称密钥流,加密消息负载 payload。
3.1) CP-ABE 的 Encrypt/Decrypt 更具体流程
为了把“策略树”真的变成可解密/不可解密的密文,我们通常把流程拆成下面几步(记用户属性集合为
Encrypt(
- 输入:
- 策略树
(阈值门 + 属性叶子) - 明文
- 策略树
- 选取随机数
。 - 计算用于加密的共享密钥:
- 生成“策略相关”的结构化密文:
- 以
为根秘密,在树上做阈值秘密共享;每个节点 得到份额 - 对每个叶子(属性
)计算并写入与该叶子关联的密文组件(把份额绑定到属性上)
- 以
- 用
派生对称密钥流,加密 得到 payload。 - 输出密文
:包含(策略树结构 + 叶子组件 + payload)。
Decrypt(
- 输入:
- 密文
(携带策略树) - 私钥
(绑定属性集合 )
- 密文
- 从策略树叶子开始尝试恢复:
- 若用户拥有叶子属性
的私钥组件,则该叶子“可用”,能计算出一个中间值(可理解为“拿到该叶子的份额贡献”)
- 若用户拥有叶子属性
- 对每个内部节点:
- 收集可用的子节点结果
- 若少于阈值
,该节点失败 - 若不少于
,用拉格朗日插值在 处聚合,得到该节点的中间值
- 若根节点失败:输出“解密失败”(属性不满足策略)。
- 若根节点成功:恢复出与
对应的聚合量,从而得到共享密钥 。 - 用
解出 payload,还原明文 。
整体流程(“如何构建 CP 控制结构并参与加密”)可以看成:
CP-ABE 的加解密过程也可以用一张“阶段流程图”概括:
4) CP-ABE 解密时“满足策略”是如何判断的?
解密可以理解为在树上做一次“自底向上”的可满足性计算:
- 叶子节点:如果用户确实拥有该属性对应的私钥组件,就能计算出一个与该叶子份额相关的中间值
- 内部节点:只要能从孩子里凑够至少
个“可用中间值”,就用拉格朗日插值在 处复原父节点中间值
所以 CP-ABE 的“访问控制结构”本质上是:
用阈值树把秘密份额分发到叶子;解密只要能在足够多叶子上拿到份额,就能插值还原。
KP-ABE:密钥侧策略树(PolicyTree)如何构建
KP-ABE 同样用“阈值策略树”来表达访问策略,但与 CP-ABE 相反:策略树不是放在密文里,而是放在私钥里:
- 密文:只携带属性集合(外加每个属性的密文组件)
- 私钥:携带一棵“策略树同形结构”,并在叶子处存放密钥组件(可理解为把策略“编译”进密钥)
1) KP-ABE 的控制结构:策略树 → 密钥树
密钥生成阶段会做一个核心转换:
- 输入:访问策略树(由 KGC/系统管理员构造)
- 输出:密钥树(结构与策略树同形,但叶子携带密钥组件)
其思想是:把主秘密
- 把主秘密
当作根秘密 - 递归按阈值门给子节点分发份额
- 在每个叶子(属性 i)生成密钥组件:
也就是说:
KP-ABE 的“访问控制结构”是由发证方在 KeyGen 时写进密钥里的。
2) 一个 KP 策略例子:至少满足 2 个属性
规则:用户能解密当且仅当密文属性集合中满足 {A,B,C} 里至少 2 个(一个 2-of-3 阈值门)。
策略树示意:
这棵树会在密钥生成阶段被“编译”进私钥结构中(即:私钥内部带着这棵策略的结构与对应的叶子密钥组件)。
3) KP-ABE 加密侧如何“构建控制结构”?
KP-ABE 加密侧不再构建策略树,它构建的是属性集合:
- 选择本次密文声明的属性集合(比如
{A, C, ...}) - 并对每个属性
计算密文组件
所以 KP-ABE 的“访问控制结构”分两步形成:
- KGC/管理员:构造策略树(控制结构)并在 KeyGen 写进密钥
- 加密者:只决定密文携带哪些属性
流程示例(“如何构建 KP 控制结构并发放密钥/加密”):
4) KP-ABE 解密是怎样“按策略验属性”的?
解密时在“密钥树”上递归:
- 到叶子节点(属性
):如果密文里确实带有该属性的组件 ,就能算出与该叶子份额对应的中间值(例如 ) - 到内部节点:如果能从孩子里凑够至少
个可用值,就通过插值恢复父节点值
所以在 KP-ABE 中:
控制结构在“密钥侧”,密文侧只要声明自己有哪些属性;能不能解密,由密钥里的策略树决定。
5) KP-ABE 的 Encrypt/Decrypt 更具体流程
把 KP-ABE 看成“策略在钥匙上、属性在锁上”会更直观。
设策略树为
Encrypt(
- 输入:
- 属性集合
- 明文
- 属性集合
- 选取随机数
。 - 计算共享密钥:
- 对每个属性
生成密文组件: - 用
派生对称密钥流,加密 得 payload。 - 输出密文
。
Decrypt(
- 输入:
- 密文
(属性集合 与组件 ) - 私钥
(携带策略树结构,并在叶子处带对应密钥组件)
- 密文
- 在“密钥侧策略树”上递归:
- 叶子节点对应属性
:若 ,则可计算该叶子的中间值(例如 ) - 内部节点:若可用子节点数量达到阈值,用拉格朗日插值聚合
- 叶子节点对应属性
- 若根节点失败:输出“解密失败”(密文属性不满足密钥策略)。
- 若根节点成功:恢复共享密钥
。 - 用
解出 payload,还原明文 。
KP-ABE 的加解密过程概括如下: