Week 2：完美安全、流密码、分组密码

完美安全

定义

对于在空间 $(\mathbb{K},\mathbb{M},\mathbb{C})$ 上的算法E，对于任意的 $m_1,m_2 \in \mathbb{M}, |m_1|=|m_2|$ ，任意的 $c \in \mathbb{C}$ ，都有：

$\frac{\#\{k \in \mathbb{K} : E(k,m_1)=c\}}{|\mathbb{K}|} = \frac{\#\{k \in \mathbb{K} : E(k,m_2)=c\}}{|\mathbb{K}|} = \frac{1}{|\mathbb{K}|}$

解释：对于任意两个等长的明文$m_1$和$m_2$，以及任意一个密文$c$，使用随机选择的密钥加密$m_1$得到$c$的概率，等于使用随机选择的密钥加密$m_2$得到$c$的概率，且都等于$\frac{1}{|\mathbb{K}|}$。

就是说对于任意一条明文，在对于一个密钥对应的密文空间映射中，每一个密文出现的概率都是均等的。

One-Time Pad

对于一次一密来说，当$|\mathbb{K}| \geq |\mathbb{M}|$时，既密钥长度大于等于明文长度时，一次一密可以达到完美安全。

为什么当密钥长度小于明文长度时不完美安全

假设$|\mathbb{K}| < |\mathbb{M}|$，则存在$m_1,m_2 \in \mathbb{M}, |m_1|=|m_2|$，使得$m_1 \oplus k = m_2 \oplus k$，即$m_1 = m_2$，与$m_1 \neq m_2$矛盾。

为什么Two-Time Pad不安全

C_1 \leftarrow M_1 \oplus K \\ C_2 \leftarrow M_2 \oplus K \\

$C_1 \oplus C_2 = M_1 \oplus M_2$

则由于编码大多是ASCII编码，则可以通过$M_1 \oplus M_2$的关系进行破解。

流密码

由于在工程实现中，一次一密要求的$\mathbb{K} \geq \mathbb{M}$显然难以实现，所以引入了伪随机数生成器PRNG来扩展密钥以求近似一次一密的效果。

PRG的安全性：不可预测性(Unpredictable)

对于算法$G:\{0,1\}^s \rightarrow \{0,1\}^n$，其中$s<n$，如果对于任意的$i<n$，给定$G(k)_1,G(k)_2,...,G(k)_i$，无法以非忽略概率预测出$G(k)_{i+1}$，则称$G$是不可预测的。

既对于已知前一个比特或者前n个比特，预测出下一个比特的概率是否大于1/2。

Pr[A(G(k)_{1,\dots,i}) = G(k)_{i+1}] \leq \frac{1}{2} + \varepsilon

当$\varepsilon = \frac{1}{2^{32}}$时，认为是不可预测的。

更多定义

PRG的安全性：不可区分性(Indistinguishability)

伪随机数生成器的定义

既在真随机数空间 $\{0,1\}^n$中，伪随机数只占据其中一个子集。

统计测试

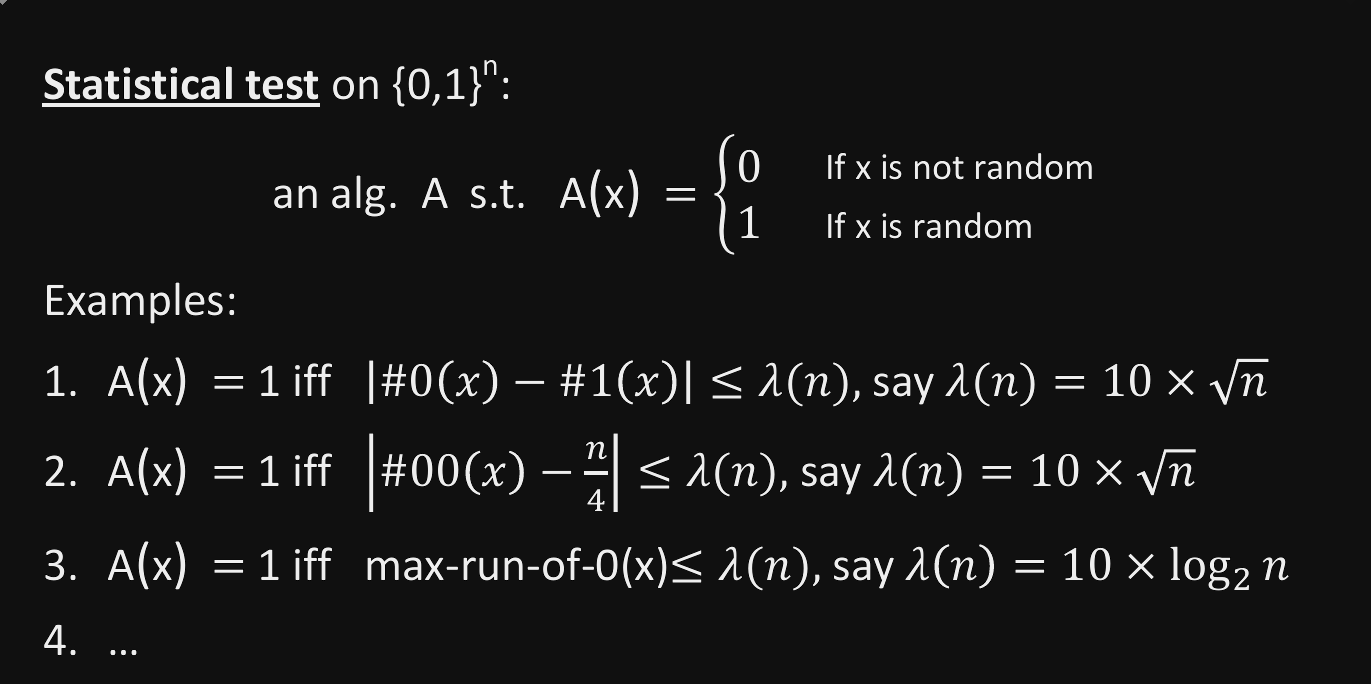
定义

假设$G:k \rightarrow \{0,1\}^n$ ，既G是一个生成n比特的随机数生成器，并且存在一个统计测试$A$，定义：

$PRG_{adv}[A,G] = |Pr[A(G(k))=1] - Pr[A(r)=1]| \in [0,1]$

• 如果优势Adv接近1，则说明$G(k)$和$r$很容易区分，$G$不是一个好的伪随机数生成器。
• 如果优势Adv接近0，则说明$G(k)$和$r$很难区分，$G$是一个好的伪随机数生成器。

则如果对于任意的统计测试$A$，优势$PRG_{adv}$是可忽略的，则称PRG是安全的具有不可区分性的

Add-on

 

 

语义安全

对于在空间 $\mathbb{K,M,C}$ 上的加密算法E:

E是完美安全的，当: $\{E(k,m_1)\} = \{E(k,m_2)\}$ , 既密文的分布概率是完全相等的

E是语义安全的，当: $\{E(k,m_1)\} \approx \{E(k,m_2)\}$ , 既密文的分布概率是计算性不可区分的

分组密码

PRF和PRP

PRF和PRP的区别在于，PRP是一个双射函数，既每一个输入对应唯一的输出，每一个输出也对应唯一的输入，而PRF则没有这个要求。

 

安全的PRF

安全的PRF

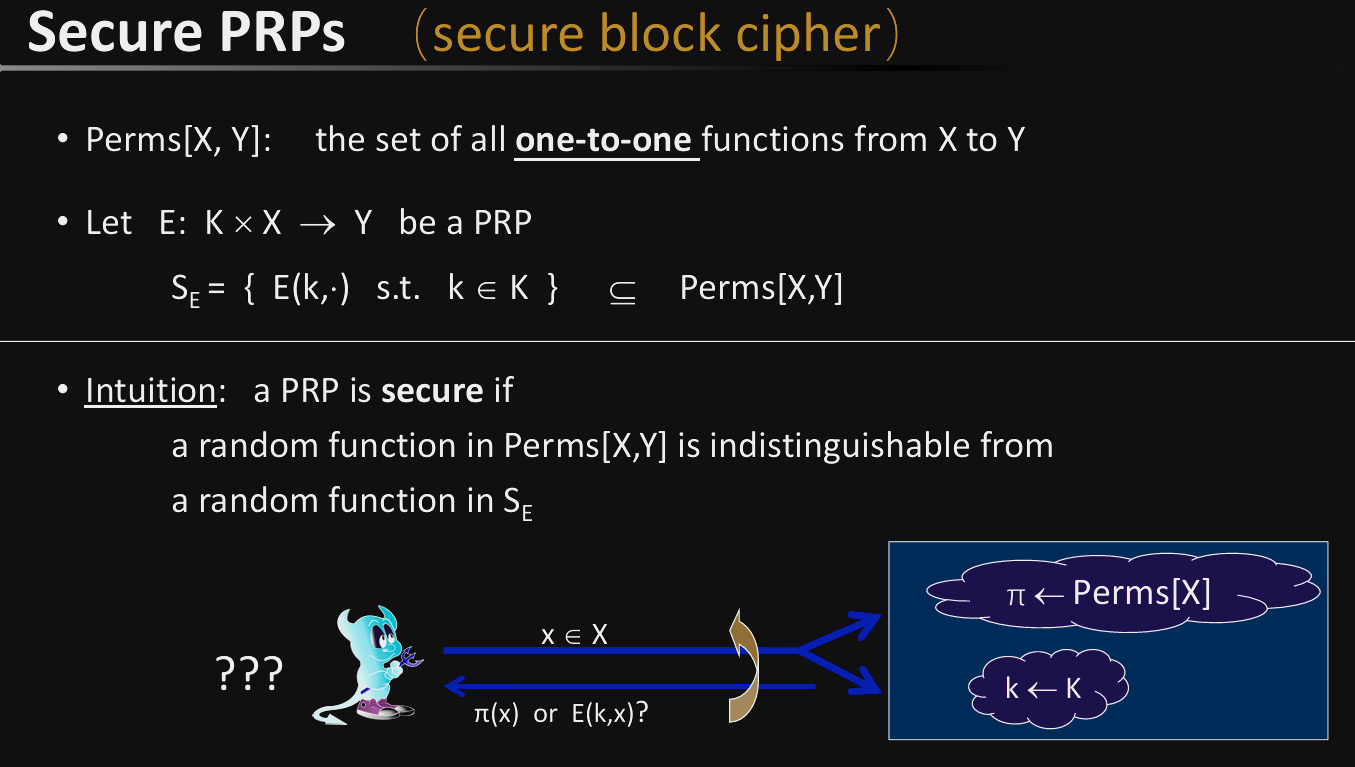
安全的PRP

安全的PRP

既对于一个安全的PRP，攻击者无法区分它和一个随机置换。