安全多方计算复

1. 安全两方计算背景

百万富翁问题

问题描述：两个百万富翁Alice和Bob想知道谁更富有，但又不愿意让对方知道自己拥有的真正财富。如何在没有第三方的情况下，让对方知道谁更有钱？

解决方案：假设Alice有$x_a$，Bob有$x_b$，他们要共同计算函数$f(x_a,x_b)$，在计算函数$f$后，他们能知道谁更富有。

函数定义：

$$f(x_a,x_b)=\{\begin{array}{ll}1& \text{if }{x}_a\ge x_b\\ 0& \text{if }{x}_a<x_b\end{array}$$

基本思想：安全两方计算（Secure two-party computation）是安全多方计算的一个子问题，目标是创建一个通用协议，该协议允许在保护双方输入值的前提下，两方共同计算一个任意函数。

历史背景：姚期智先生最早提出了基于混淆电路的两方安全计算通用协议，可以实现对任意类型布尔门电路的安全计算。

2. 姚氏混淆电路

基本原理

假设需要计算函数 $g(x,y)$，其中 $g$代表布尔电路的单个门，且它的输入为$x,y\in \{0,1\}$ 。

对每个输入$x,y$，可以分为两种情况，即：

• $x:(x_1,x_2)$，分别对应于值取0和1
• $y:(y_1,y_2)$，分别对应于值取0和1

在姚氏混淆电路中，参与双方需分别负责构造混淆电路和计算混淆电路。假设参与者分别是Alice和Bob，并且Alice负责构造混淆电路，Bob负责计算混淆电路。

混淆表构造

Alice对 $x,y$产生两个对称密钥，即$x_1,x_2,y_1,y_2$ 分别对应 $k_{x_1},k_{x_2},k_{y_1},k_{y_2}$。然后Alice构造混淆表：

$k_{x_i}$	$k_{y_j}$	$E_{k_{x_i}}(E_{k_{y_j}}(g(x_i,y_j)))$
$k_{x_1}$	$k_{y_1}$	$E_{k_{x_1}}(E_{k_{y_1}}(g(x_1,y_1)))$
$k_{x_1}$	$k_{y_2}$	$E_{k_{x_1}}(E_{k_{y_2}}(g(x_1,y_2)))$
$k_{x_2}$	$k_{y_1}$	$E_{k_{x_2}}(E_{k_{y_1}}(g(x_2,y_1)))$
$k_{x_2}$	$k_{y_2}$	$E_{k_{x_2}}(E_{k_{y_2}}(g(x_2,y_2)))$

• Alice有 $x_1$，则她将打乱顺序的混淆表和 $k_{x_1}$ 发给Bob。
• 假设Bob有$y_2$，Bob和Alice运行OT ${}_2^1$协议，可以得到$y_2$ 对应的 $k_{y_2}$，然后使用$k_{x_1}$ 和 $k_{y_2}$ 可以解密 $E_{k_{x_1}}(E_{k_{y_2}}(f(x_1,y_2)))$ 得到$g(x_1,y_2)$并将其发送给Alice。

与门电路示例

问题：Alice和Bob分别有$x$和 $y$，两方想在不泄露自己的输入的情况下准确计算 $x\wedge y$。

密钥设置：

• $x$ 对应的密钥为 $(k_{x_0},k_{x_1})$-$y$ 对应的密钥为 $(k_{y_0},k_{y_1})$- 输出线$z$ 对应的密钥为 $(k_{z_0},k_{z_1})$

与门电路真值表：

$x$	$y$	$x\wedge y$
0	0	0
0	1	0
1	0	0
1	1	1

输出转换表：

$k_z^e$	$z$
$k_z^0$	0
$k_z^1$	1

混淆表：

$k_{x_i}$	$k_{y_j}$	$C_d=E_{k_{x_i}}(E_{k_{y_j}}(k_z^e))$
$k_{x_0}$	$k_{y_0}$	$C_0=E_{k_{x_0}}(E_{k_{y_0}}(k_z^0))$
$k_{x_0}$	$k_{y_1}$	$C_1=E_{k_{x_0}}(E_{k_{y_1}}(k_z^0))$
$k_{x_1}$	$k_{y_0}$	$C_2=E_{k_{x_1}}(E_{k_{y_0}}(k_z^0))$
$k_{x_1}$	$k_{y_1}$	$C_3=E_{k_{x_1}}(E_{k_{y_1}}(k_z^1))$

执行过程：

• 假如$x=0$，$y=1$，则Alice将$k_{x_0}$和混淆表发给Bob。
• 双方运行OT协议，Bob得到$k_{y_1}$。
• 然后使用 $k_{x_0}$ 和 $k_{y_1}$ 可以解密 $C_1$ 得到 $k_{z_0}$。
• 根据输出转换表，得到 $k_{z_0}$ 的真值0。

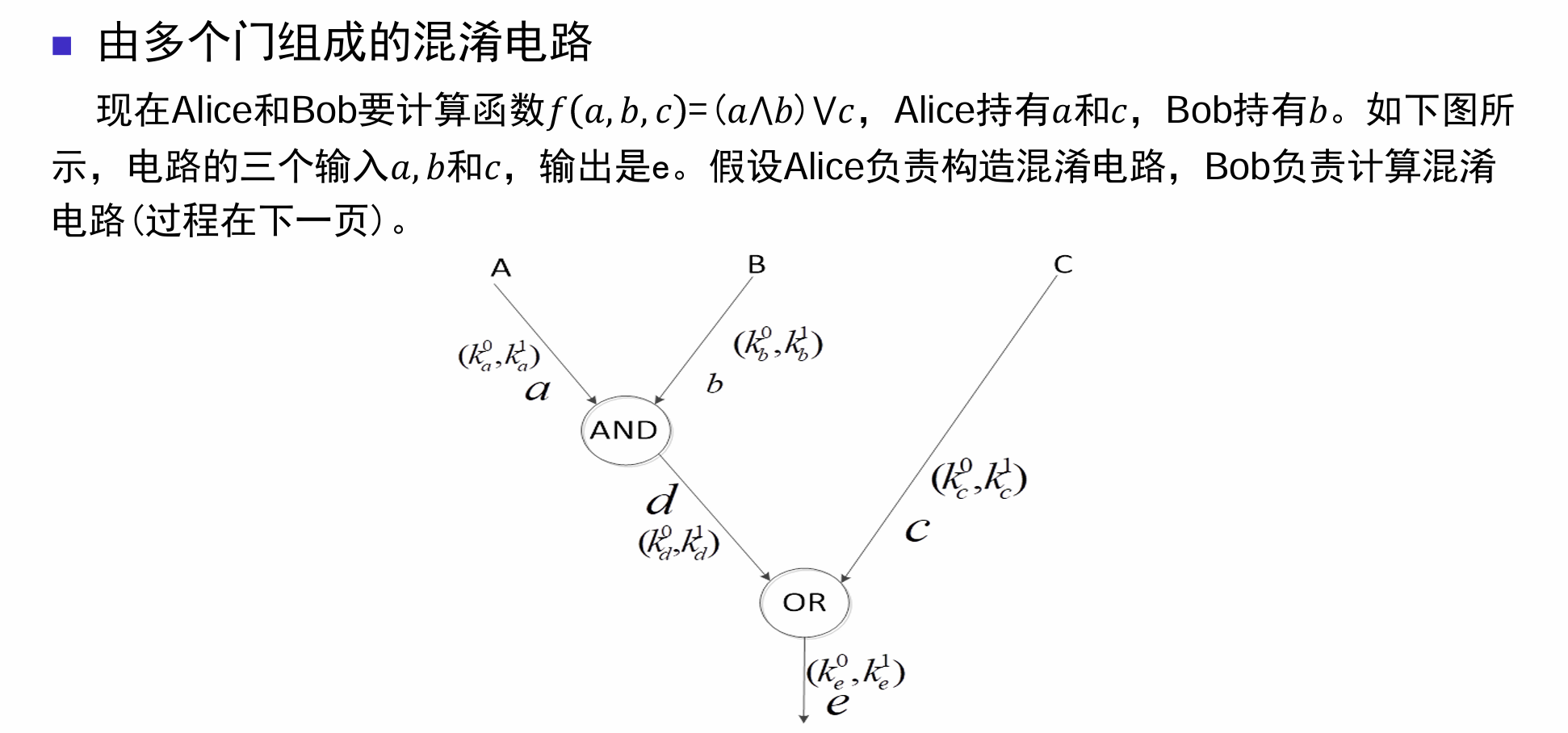
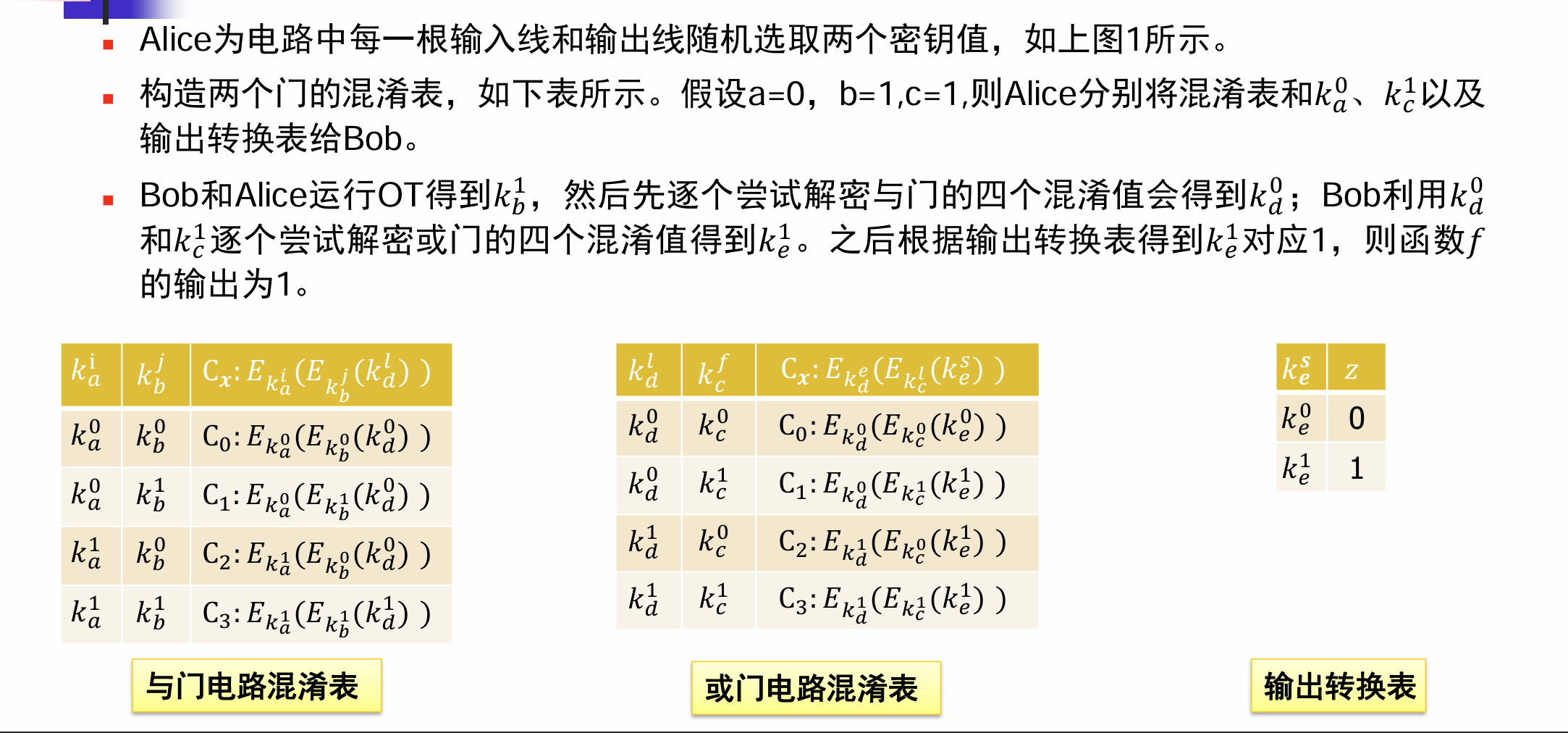
多个门组成的混淆电路

• 
• 

混淆电路的优化 - Point and Permute

问题：在上述混淆电路中，当接收方收到四个混淆值时要尝试解密直到成功为止，存在一定的开销。

优化方法：Point-and-Permute方法，可以帮助接收者定位到要解密的密文，只需要解密一次。

优化步骤：

1. 令每个门输入 $x,y$ 和输出 $z$的两个密钥中都加1bit指针位$p$ ，即：

   • 对于输入$x$：它原本对应的密钥是 $k_{x_0},k_{x_1}$，引入一bit指针位 $p_x$，$p_x\in \{0,1\}$，此时的密钥变为 $(k_{x_0}\Vert p_{x_0})$ 和 $(k_{x_1}\Vert p_{x_1})$，其中$p_{x_0}\oplus p_{x_1}=1$。
   • 同上，对于输入$y$，两个密钥变为 $(k_{y_0}\Vert p_{y_0})$ 和 $(k_{y_1}\Vert p_{y_1})$，$p_{y_0}\oplus p_{y_1}=1$。
   • 对于输出$z$，两个密钥变为$(k_{z_0}\Vert p_{z_0})$ 和 $(k_{z_1}\Vert p_{z_1})$，$p_{z_0}\oplus p_{z_1}=1$。

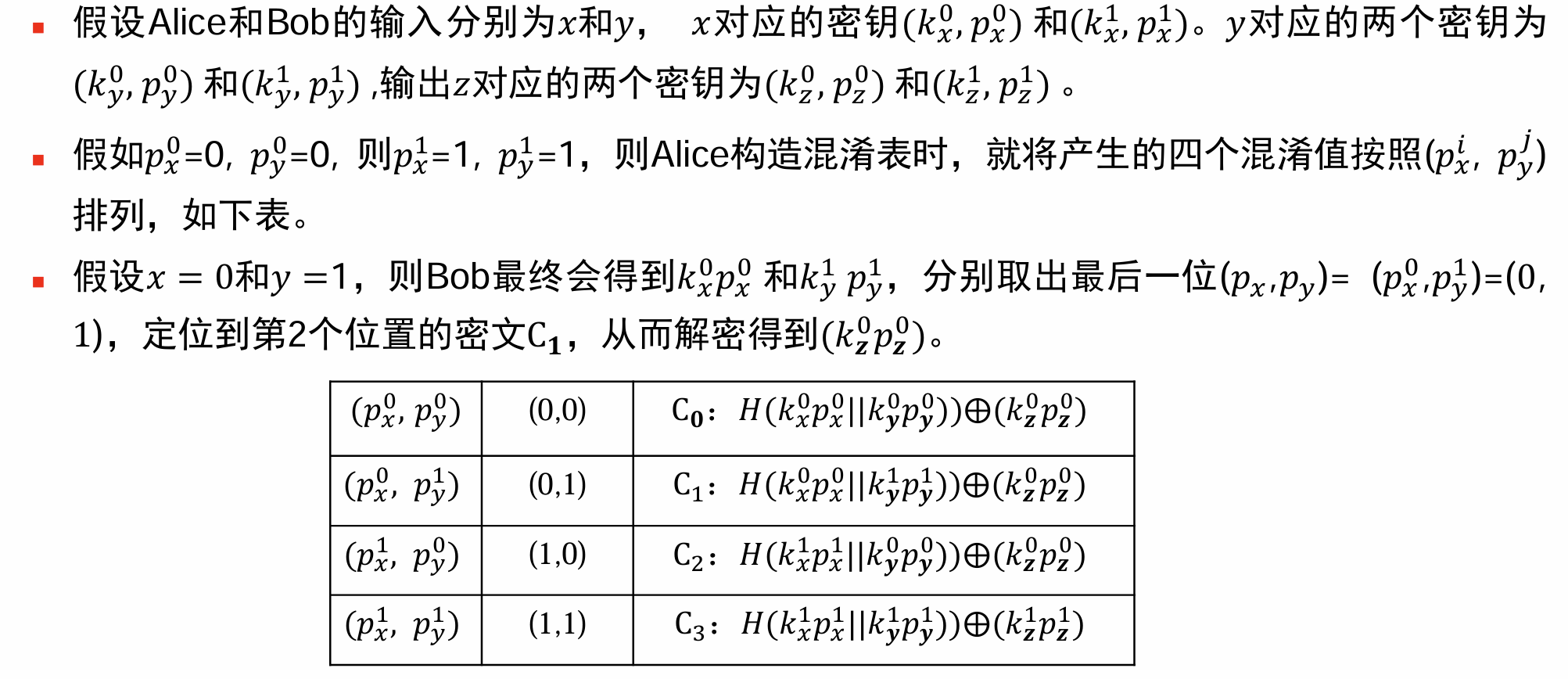
2. Alice构造混淆表时，表中的每一项按照两个密钥的最后一位$(p_{x_i},p_{y_j})$的值排列，然后发送给Bob。

3. Bob收到混淆表和与Alice输入对应的$k_x$后，与Alice运行OT协议得到$k_y$。

4. Bob分别将$k_x$和 $k_y$的最后1 bit$p_x$和 $p_y$取出，以$(p_x,p_y)$ 为坐标在混淆表中找到相应的密文进行解密，即可得到正确的$k_z$。

与门示例：

• 

3. GMW协议

GMW协议简介

GMW协议(Goldreich-Micali-Wigderson)是由Goldreich等人提出，是一种支持安全多方计算的协议。GMW协议通常采用秘密分享及OT等常见的密码学原语来实现多方的安全计算功能。

与Yao氏混淆电路协议略有不同，GMW协议不但支持布尔电路还支持算术电路。同时，电路评估时不再使用混淆表，而是在本地直接进行计算，这样大大节省对混淆真值表带来的解密操作，可以减少计算量，节省计算成本。

异或门

秘密分享：

• Alice和Bob的输入分别为$x_a$、$x_b$。
• Alice产生随机数$r_a$，Bob产生随机数$r_b$，则$x_a$的两个子份额分别为$\{x_a\oplus r_a,r_a\}$，其中Alice持有$x_a\oplus r_a$，Bob持有$r_a$，两个子份额异或可得$x_a$。
• 同理将Bob的子份额进行分享，Alice会得到$r_b$，Bob持有$x_b\oplus r_b$。

计算过程：

• 双方分别在本地将 $x_a$ 、$x_b$ 的子份额异或：
  • Alice: $x_a\oplus r_a\oplus r_b$
  • Bob:$x_b\oplus r_b\oplus r_a$
• 而$(x_a\oplus r_a\oplus r_b)\oplus (x_b\oplus r_b\oplus r_a)=x_a\oplus x_b$，因此最终双方会各持有一份$x_a\oplus x_b$的子份额。

与非门(不需要交互)

秘密分享：

• 分享Alice的输入$x$，Alice选取随机数$r$，并将$r$发送给Bob，则$x$的两个子份额分别为$\{x\oplus r,r\}$，其中Alice持有$x\oplus r$，Bob持有$r$。

计算过程：

• Alice在本地将持有的子份额取反，即Alice: $x\oplus r$。
• 因为$(x\oplus r)\oplus r=\overline{x}$，所以最终Alice和Bob各有一份$\overline{x}$的子份额。

与门

秘密分享：

• Alice持有子份额$(x_1,y_1)$，Bob持有子份额$(x_2,y_2)$。
• Alice会针对Bob的子份额的可能取值(0或1)，构造一个表$T_1$，即$f=(x_1\oplus x_2)\wedge (y_1\oplus y_2)$。

表$T_1$:

$x_2$	$y_2$	$S_{x_2,y_2}=f(x_1,x_2,y_1,y_2)$
0	0	$S_{00}$: $f(x_1,0,y_1,0)$
0	1	$S_{01}$: $f(x_1,0,y_1,1)$
1	0	$S_{10}$: $f(x_1,1,y_1,0)$
1	1	$S_{11}$: $f(x_1,1,y_1,1)$

表$T_2$:

• Alice随机选择一个$r\in \{0,1\}$，并将$T_1$表中每一项均与$r$异或得到表$T_2$。
• $T_2$: $S_{00}:r\oplus f(x_1,0,y_1,0)$, $S_{01}:r\oplus f(x_1,0,y_1,1)$, $S_{10}:r\oplus f(x_1,1,y_1,0)$, $S_{11}:r\oplus f(x_1,1,y_1,1)$

执行过程:

• Alice和Bob运行OT${}_4^1$协议，其中Alice充当发送方，Bob充当接收方。
• Alice准备的四个消息为$(S_{00},S_{01},S_{10},S_{11})$，Bob以$(x_2,y_2)$作为选择位。
• 最终Bob会得到$x\wedge y$的子份额$r\oplus x\wedge y$，Alice有子份额$r$，而$r\oplus r\oplus x\wedge y=x\wedge y$，所以Alice和Bob各得到$x\wedge y$的一个子份额。

从两方扩展到多方

秘密分享：

• 假设有$n$个用户$P_1,P_2,...,P_n$，每个用户$P_i$的隐私输入为$x_i$。
• 用户$P_i$分享$x_i$的过程如下：
  • $P_i$随机选取$n-1$个随机数$r_{i1},r_{i2},...,r_{i(n-1)}$作为$x_i$的前$n-1$子份额$\{x_{i1},x_{i2},...,x_{i(n-1)}\}$。
  • 第$n$个子份额$x_{in}=r_{i1}\oplus r_{i2}\oplus ...\oplus r_{i(n-1)}\oplus x_i$。
  • 对这$n$个子份额进行异或操作可恢复得到$x_i$。
  • $P_i$ 把 $r_{i1},r_{i2},...,r_{i(n-1)}$ 分别发给 $n-1$ 个用户，自己保留第$n$ 个子份额 $x_{in}$ 。

异或门计算：

• 用户$P_i$本地计算$z_i=x_i\oplus y_i$。
• 则$z=x\oplus y=(x_1\oplus ...\oplus x_n)\oplus (y_1\oplus ...\oplus y_n)={\oplus }_{i=1}^n{z}_i$。
• 即参与者$P_i$在本地计算所得到的$z_i$就是$P_i$在该异或门输出信号线$z$上的秘密份额。

与门计算：

• $x\wedge y=(x_1\oplus ...\oplus x_n)\wedge (y_1\oplus ...\oplus y_n)={\oplus }_{i=1}^n(x_i\wedge y_i)\oplus ({\oplus }_{i\ne j}{x}_i\wedge y_j)$。
• 用户$P_i$本地计算$x_i\wedge y_i$，则可获得${\oplus }_{i=1}^n{x}_i\wedge y_i$的一个子份额。
• 用户$P_i$持有$x_i$，用户$P_j$持有$y_j$，$ P_i $ 和 $P_j$ 分别输入 $x_i$ 和 $y_j$ 运行GMW的两方安全的与门协议，则每一方可以得到 $x_i\wedge y_j$ 的子份额，表示为 $[x_i\wedge y_j]$。
• 各个参与方在本地将两个部分的子份额 $x_i\wedge y_i$ 和 $[x_i\wedge y_j]$ 异或得到 $x\wedge y$ 的子份额，即：$$(x_i\wedge y_i)\oplus ({\oplus }_{i\ne j}[x_i\wedge y_j])$$

4. BGW协议

BGW协议简介

BGW协议利用Shamir提出的$(t,n)$门限秘密共享方法实现安全多方计算。假设存在$n$个用户$P_1,P_2,...,P_n$，其中用户$P_i$持有秘密$a_i$。

秘密分享：

• 用户$P_i$选取一个$t-1$阶的多项式$f_i$，且$f_i(0)=a_i$。
• 则用户$P_i$持有$n$个秘密的共享份额$[a_j{]}_i=f_j(i)$，$1\le j\le n$。
• 最终各个参与方的子份额如下表所示：

$P_1$	$a_1$	$f_1(1)$	$f_2(1)$	...	$f_n(1)$
$P_2$	$a_2$	$f_1(2)$	$f_2(2)$	...	$f_n(2)$
...	...	...	...	...	...
$P_n$	$a_n$	$f_1(n)$	$f_2(n)$	...	$f_n(n)$

加法运算

计算 $a=[a_1+a_2+\cdots +a_n]$:

• $P_i$本地计算$f(i)=f_1(i)+f_2(i)+...+f_n(i)$，则$[a{]}_i=f(i)$。

乘法运算

计算 $a=[a_1\cdot a_2]$:

• $P_i$本地计算$f(i)=f_1(i)\cdot f_2(i)$。

• 注意：多项式$f(x)$的阶为$2(t-1)$，故需要$2t-1$个份额才能恢复多项式，因此需要降阶到$t-1$阶，方法如下：

  $$f^0=\sum _{i=1}^{2t-1}{\lambda }_{i}f(i)$$

  其中${\lambda }_i$是拉格朗日系数。

• $P_i$选取一个新的$t-1$阶的多项式$f_i^{\prime }(x)$，且$f_i^{\prime }(0)=f(i)$。

• $P_i$有 $n$ 个份额 ${\lambda }_i{f}_1^{\prime }(i),{\lambda }_i{f}_2^{\prime }(i),...,{\lambda }_i{f}_n^{\prime }(i)$，然后本地计算：

  $${\lambda }_i{f}_1^{\prime }(i)+{\lambda }_i{f}_2^{\prime }(i)+...+{\lambda }_i{f}_n^{\prime }(i)={\lambda }_i{f}_i$$

• 则$[a{]}_i={\lambda }_i{f}_i$。

乘法三元组

乘法三元组（Multiplication Triples）又被称为Beaver triple，其主要思想是利用预先在离线阶段生成的三元组实现在线时的乘法运算。

假设：参与者 $P_0$ 和 $P_1$ 已经共享随机数 $u,v$ 和 $z=uv$，即$P_i$持有$u_i,v_i,z_i$，$i\in \{0,1\}$。

计算 $c=ab$，其中$P_i$持有$a_i,b_i$，$i\in \{0,1\}$:

1. $P_i$ 本地计算 $[e{]}_i=a_i-u_i$ 和 $[f{]}_i=b_i-v_i$，并发送 $[e{]}_i$ 和$ [f]i $\mathrm{给}$P$。
2. $P_i$重构$e=[e{]}_0+[e{]}_1$和 $f=[f{]}_0+[f{]}_1$。
3. $P_i$计算$[c{]}_i=e\cdot f+f\cdot a_i+e\cdot b_i+z_i$，则参与者$P_0$和 $P_1$ 可以分别获得结果$ab$的子份额 $[c{]}_0$ 和 $[c{]}_1$。