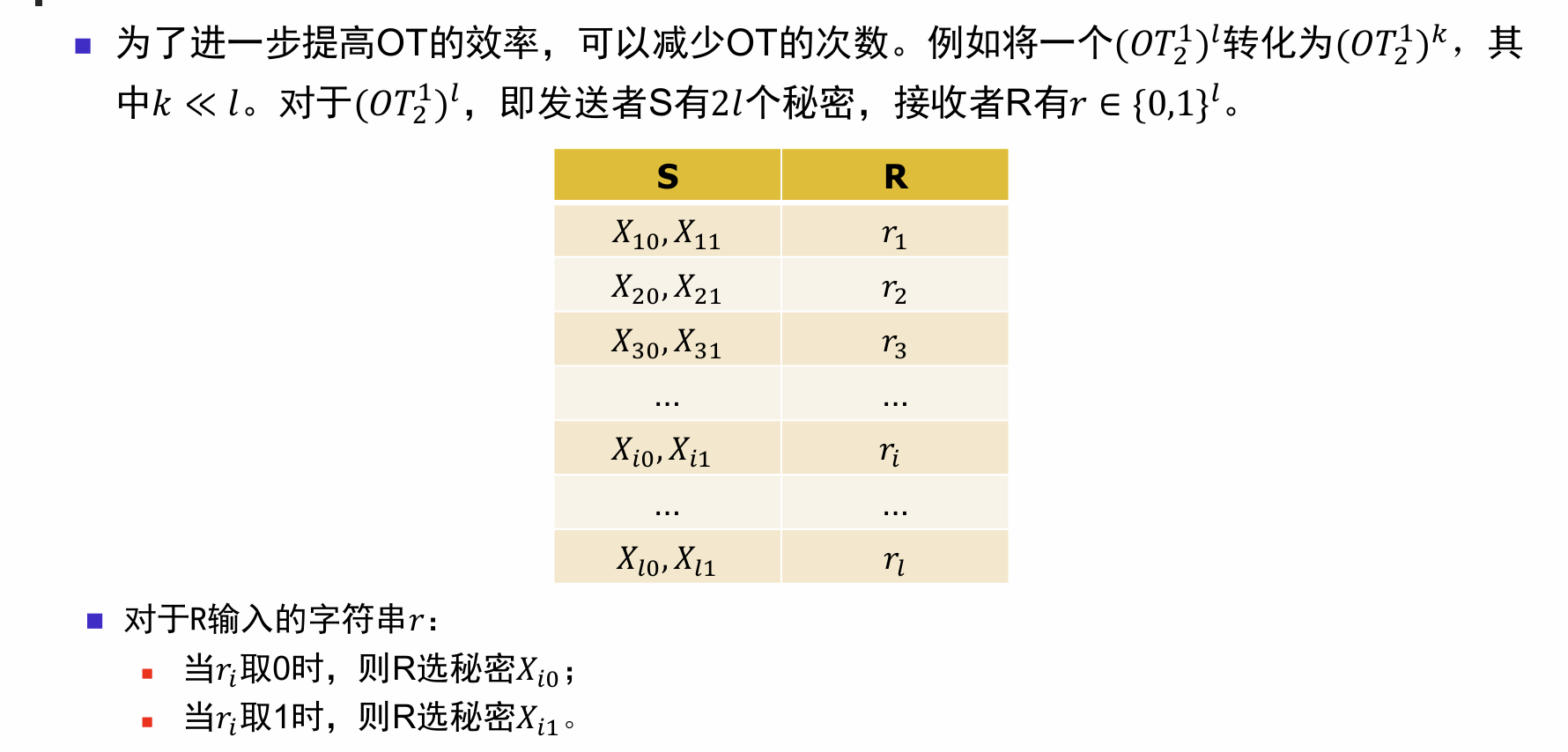
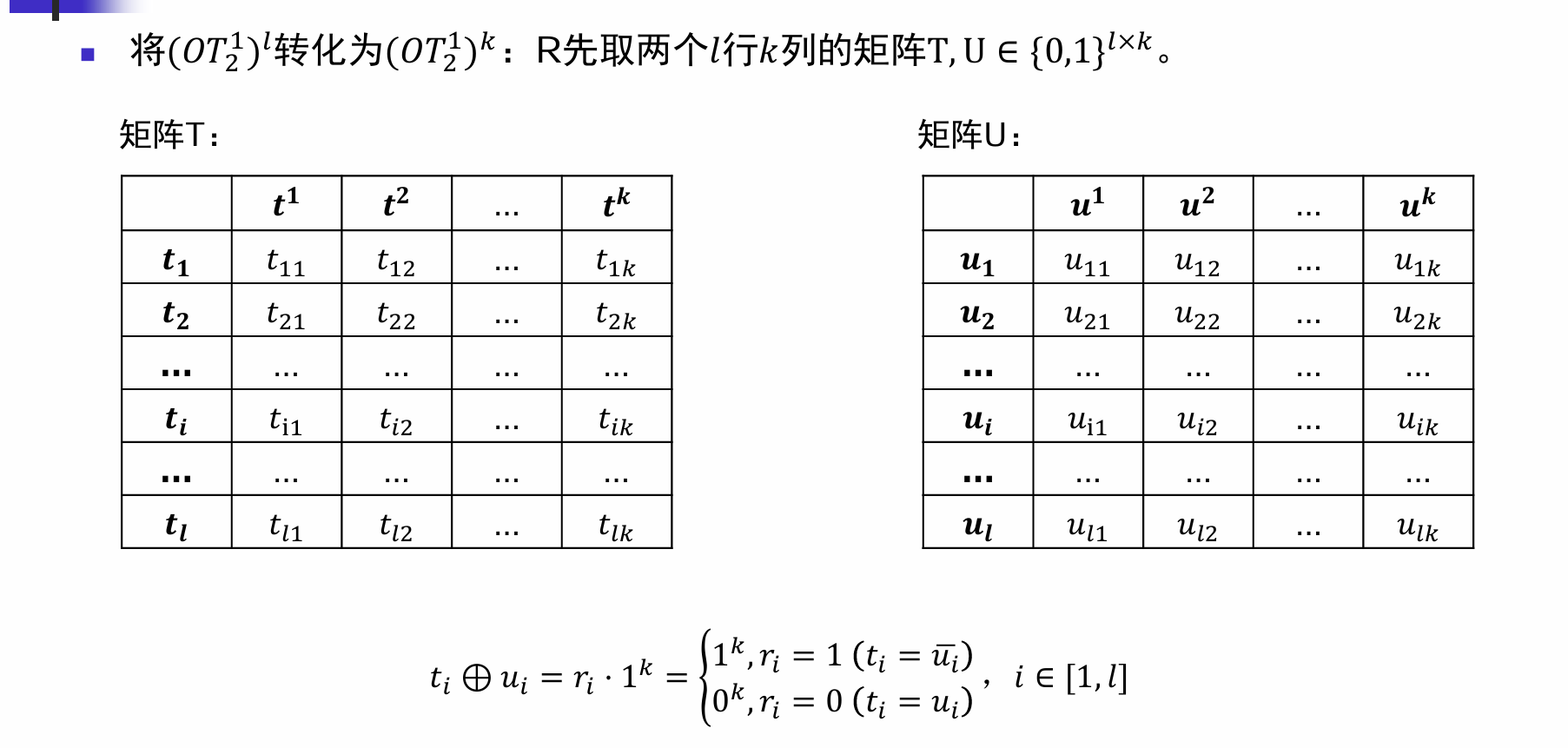
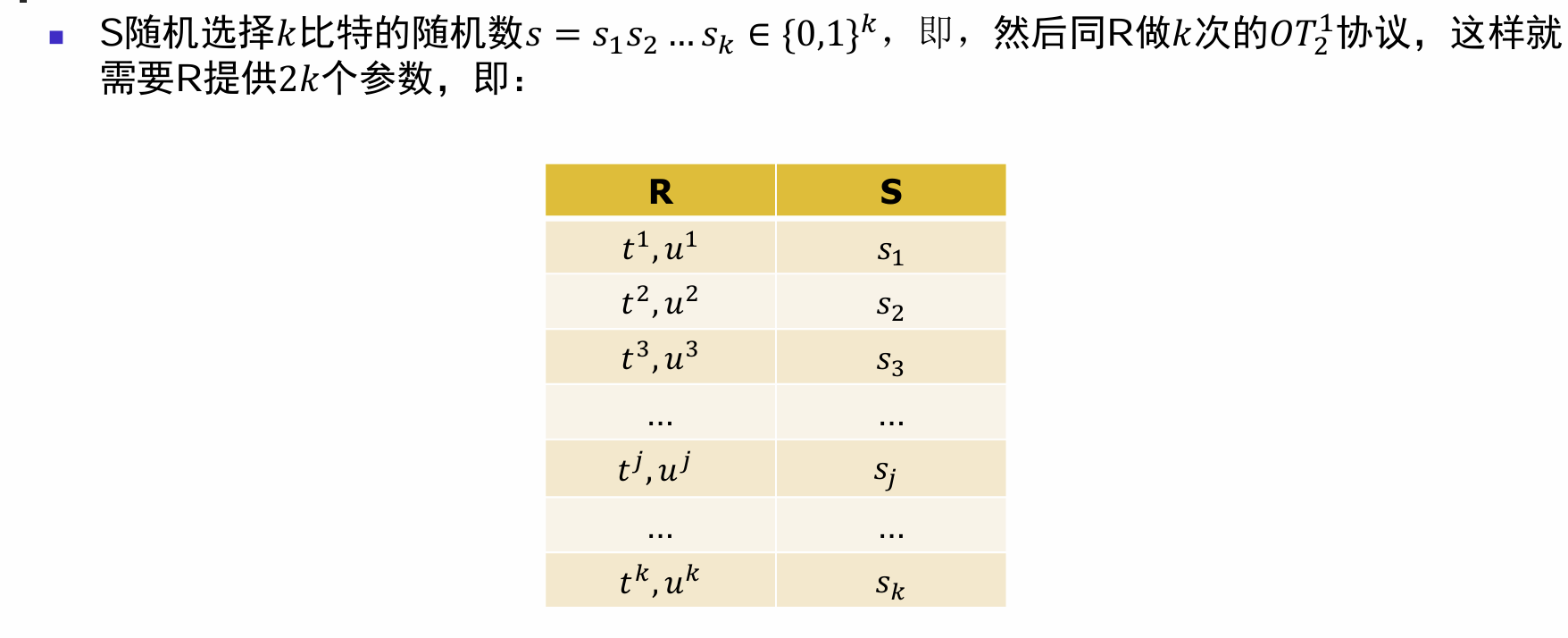
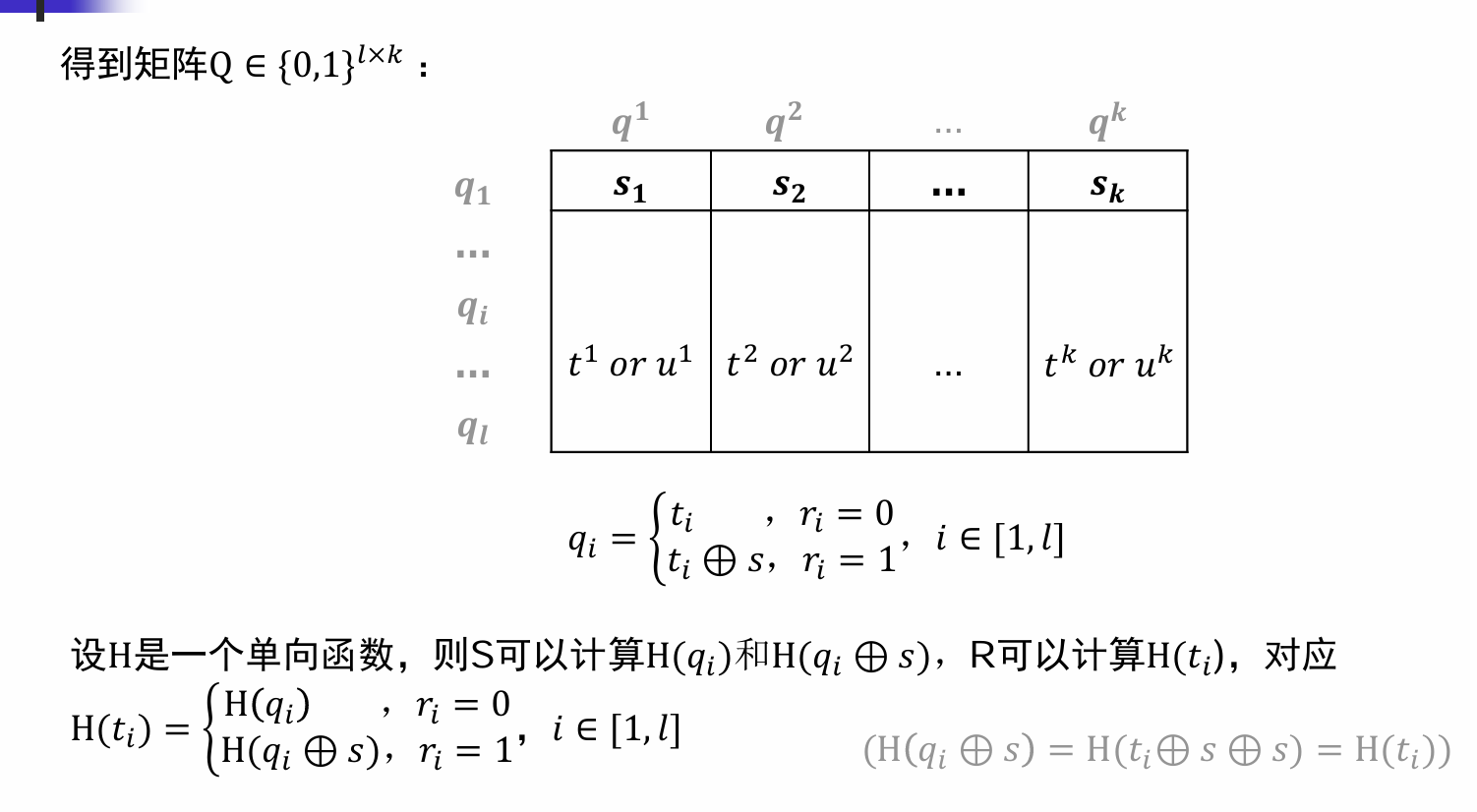
Appearance
不经意传输
Oblivious Transfer(OT).
假设 Ob一串字母小姐 有两个秘密 Doloris小姐一个秘密 Doloris小姐 不想让 Ob一串字母小姐 知道她买的是 Ob一串字母小姐 也不想让 Doloris小姐 知道另一个秘密
OT^1_2
Sheme-1
首先,我们假设接收者
: 选定他要选择的秘密 ,并生成公私钥对 ,然后随机选择一个随机数作为另一个公钥 ,并将 发送给发送者 。 : 收到公钥对 后,使用公钥 和 分别加密秘密 和 ,得到密文 和 ,然后将密文对 发送给接收者 。 : 使用私钥 解密密文 ,得到秘密 。
显然,
Sheme-2
但是,在上面的协议中,
以下以 Elgamal 为例:
:对于 , 生成群参数 ,并且再生成一个随机元素 , 把四元组 发送给 。 : 选择一个随机数 ,并且根据他想要的秘密 计算公钥对 ,然后计算另一个公钥 (此处不计算也可),并将 发送给 。 : 由 计算 。计算 和 ,这部分可以用同一个随机数掩码 来加密,叫做重用随机数,得到密文对 并发送给 。 : 使用私钥 解密密文 ,得到秘密 。
同样也是显然的,
OT^{1}_n
利用陷门置换(Trapdoor Permutation)的
假设
步骤1:秘密的传输
将 Trapdoor Permutation 发送给 ,自己保留 Trapdoor 可用来求出 的原像 。 - 设
想得到的是秘密 ,他从 的定义域中选取 个随机值 ,并将 元组 发送给 ,其中 利用 Trapdoor 计算 ,并将 发送给 ( )。
步骤2:秘密的恢复(假设B是半诚实的)
因为
什么叫半诚实的?
半诚实 (Semi-Honest) 模型,也称为 诚实但好奇 (Honest-but-Curious) 模型。
在此模型中,假设参与者(这里指 B)会:
- 诚实地 遵守协议的所有步骤(例如:在步骤 1 中,对于
,B 确实是随机选取 ,而不是精心构造的:简单地说,就是对于 我仍然使得 。 - 好奇地 尝试从收到的消息中推断出额外的隐私信息。
如果 B 是 恶意 (Malicious) 的,他可以在步骤 1 中作弊:对于